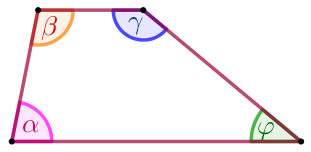
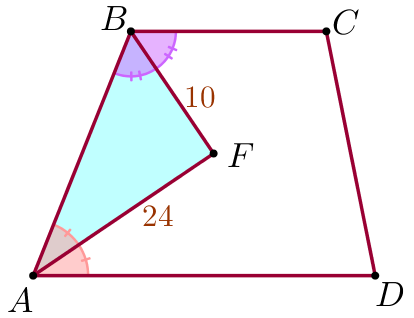
Биссектрисы углов \(\displaystyle A\) и \(\displaystyle B\) при боковой стороне \(\displaystyle AB\) трапеции \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle F {\small.}\) Найдите \(\displaystyle AB {\small,}\) если \(\displaystyle AF=24 {\small,}\) \(\displaystyle BF=10 {\small.}\)
По условию задачи выполним чертёж.
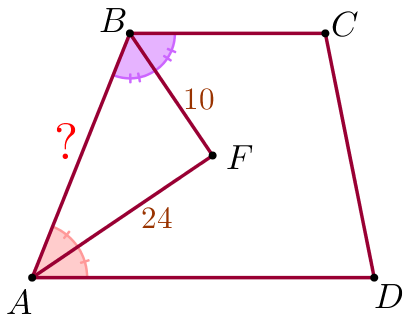 | \(\displaystyle ABCD\) – трапеция, \(\displaystyle AF=24\) – биссектриса угла \(\displaystyle A{\small,}\) \(\displaystyle BF=10\) – биссектриса угла \(\displaystyle B{\small.}\) Требуется найти длину боковой стороны \(\displaystyle AB\) трапеции \(\displaystyle ABCD{\small.}\) |
Рассмотрим прямоугольный треугольник \(\displaystyle ABF{\small:}\)
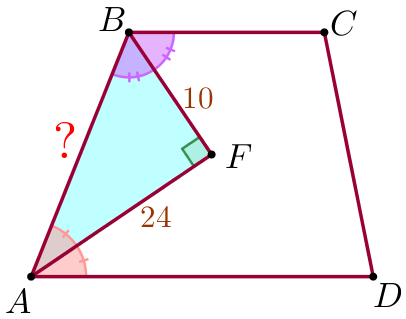 | По теореме Пифагора \(\displaystyle AB^2=AF^2+BF^2{\small,}\) \(\displaystyle AB^2=24^2+10^2=576+100=676{\small.}\) Так как длина отрезка не может быть отрицательной, то \(\displaystyle AB=\sqrt{676}=26{\small.}\) |
Ответ: \(\displaystyle 26{\small.}\)