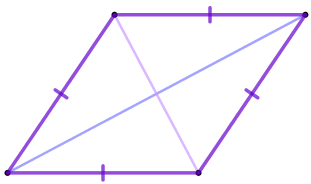
Высота \(\displaystyle AH\) ромба \(\displaystyle ABCD\) делит сторону \(\displaystyle CD\) на отрезки \(\displaystyle DH=15\) и \(\displaystyle CH=2 {\small.}\) Найдите высоту ромба.
По условию задачи выполним чертёж.
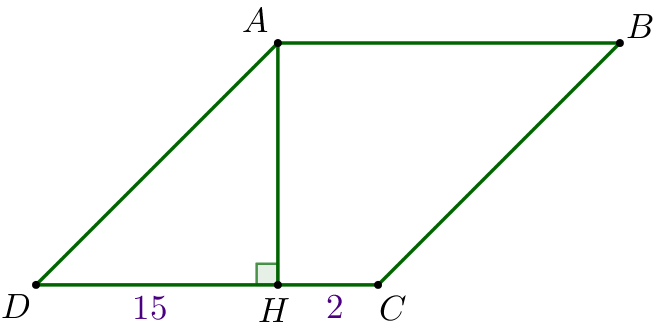 | \(\displaystyle ABCD\) – ромб, \(\displaystyle AH\) – высота ромба, \(\displaystyle DH=15{\small,}\) \(\displaystyle CH=2{\small.}\) Требуется найти высоту ромба. |
Найдём сторону ромба.
Рассмотрим прямоугольный треугольник \(\displaystyle ADH{\small.}\)
По теореме Пифагора \(\displaystyle AD^2=AH^2+DH^2{\small,} \) \(\displaystyle AH^2=AD^2-DH^2{\small,} \) \(\displaystyle AH^2=17^2-15^2=289-225=64{\small.} \) | 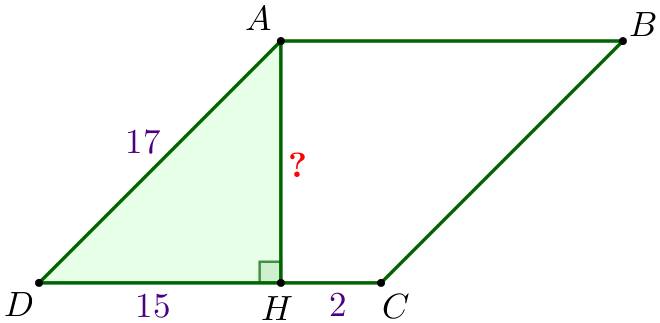 |
Так как длина отрезка не может быть отрицательной, то \(\displaystyle AH=\sqrt{64}=8{\small.}\)
Ответ: \(\displaystyle 8{\small.}\)