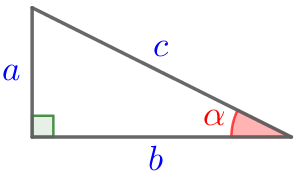
Запишите верные равенства.
| \(\displaystyle \sin 30^{\circ}=\) |
| \(\displaystyle \cos 30^{\circ}=\) |
| \(\displaystyle \tg 30^{\circ}=\) |
Рассмотрим прямоугольный треугольник \(\displaystyle ABC\) с прямым углом \(\displaystyle C\) и острым углом \(\displaystyle 30^{\circ}{\small.}\)
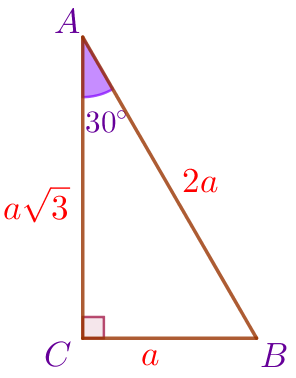 | Пусть \(\displaystyle \angle A=30^{\circ}{\small.}\) В прямоугольном треугольнике напротив угла \(\displaystyle 30^{\circ}\) лежит катет, равный половине гипотенузы. Обозначим \(\displaystyle BC=a{\small,}\) тогда \(\displaystyle AB=2a{\small.}\) С помощью теоремы Пифагора выразим \(\displaystyle AC\) через \(\displaystyle a{\small:}\) \(\displaystyle AC^2=AB^2-BC^2{\small;}\) \(\displaystyle AC^2=(2a)^2-a^2=4a^2-a^2=3a^2{\small.}\) Так как длина отрезка положительна, то \(\displaystyle AC=a\sqrt{3}{\small.}\) |
\(\displaystyle \sin 30^{\circ}=\frac{1}{2}{\small.}\)
\(\displaystyle \cos 30^{\circ}=\frac{\sqrt{3}}{2}{\small.}\)
\(\displaystyle \text{tg} \ 30^{\circ}=\frac{1}{\sqrt{3}}{\small.}\)