Основания прямоугольной трапеции равны \(\displaystyle 10\) и \(\displaystyle 4{\small .}\) Её площадь равна \(\displaystyle 14\sqrt{3}{\small .}\) Найдите острый угол этой трапеции. Ответ дайте в градусах.
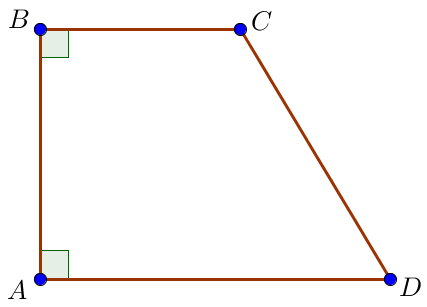
Пусть \(\displaystyle ABCD\) – прямоугольная трапеция с прямыми углами \(\displaystyle A\) и \(\displaystyle B\) и тупым углом \(\displaystyle C{\small .}\) Тогда ее основания \(\displaystyle BC=4\) и \(\displaystyle AD=10{\small,}\) большая боковая сторона \(\displaystyle CD{\small .}\) Опустим высоту \(\displaystyle CH{\small .}\) В четырехугольнике \(\displaystyle ABCH\) все углы прямые, поэтому он является прямоугольником. Значит, \(\displaystyle AH=BC=4{\small .}\) Тогда \(\displaystyle HD=AD-AH=10-4=6{\small .}\) |  |
Так как площадь трапеции равна произведению полусуммы оснований на высоту,
\(\displaystyle {S_{ABCD}} = \frac{{AD}+{BC}}{2}\cdot {CH} {\small ,}\)
то
\(\displaystyle 14\sqrt{3} = \frac{{10}+{4}}{2}\cdot {CH} {\small ,}\)
\(\displaystyle 14\sqrt{3} = 7 \cdot{CH} {\small ,}\)
откуда
\(\displaystyle {CH}=\frac{14\sqrt{3}}{7}=2\sqrt{3} {\small .}\)
Найдем острый угол \(\displaystyle CDH\) трапеции из прямоугольного треугольника \(\displaystyle CHD.\) Нам известны катеты \(\displaystyle CH=2\sqrt{3}\) и \(\displaystyle HD=6{\small .}\) \(\displaystyle CD^2=CH^2+DH^2=(2\sqrt{3})^2+6^2=12+36=48{\small .}\) Поскольку длина отрезка положительна, то \(\displaystyle CD=\sqrt{48}=4\sqrt{3}{\small .}\) Так как гипотенуза \(\displaystyle CD\) в два раза больше катета \(\displaystyle CH{\small ,}\) то против катета \(\displaystyle CH\) лежит угол \(\displaystyle 30^{\circ}{\small .}\) Значит, \(\displaystyle \angle CDH=30^{\circ}{\small .}\) | 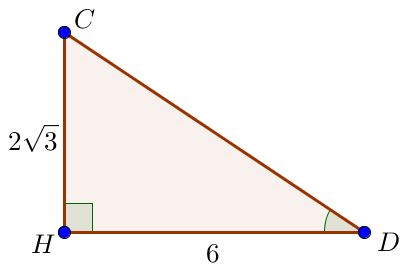 |
Ответ: \(\displaystyle 30^{\circ}{\small .}\)