Автомобильный журнал определяет рейтинг автомобилей на основе показателей безопасности \(\displaystyle S {\small ,}\) комфорта \(\displaystyle C {\small ,}\) функциональности \(\displaystyle F{\small ,}\) качества \(\displaystyle Q\) и дизайна \(\displaystyle D{\small .}\)
Рейтинг \(\displaystyle R\) вычисляется по формуле
\(\displaystyle R=\frac{3S+2C+2F+2Q+D}{50} {\small .}\)
В таблице даны показатели трёх моделей автомобилей.
| Модель автомобиля | Безопасность | Комфорт | Фукциональность | Качество | Дизайн |
| \(\displaystyle А\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 1\) | \(\displaystyle 4\) | \(\displaystyle 2\) |
| \(\displaystyle Б\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 4\) | \(\displaystyle 1\) | \(\displaystyle 5\) |
| \(\displaystyle В\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 4\) | \(\displaystyle 1\) | \(\displaystyle 1\) |
Найдите наивысший рейтинг автомобиля из представленных в таблице моделей.
Требуется найти наивысший рейтинг для представленных в таблице моделей автомобилей.
Рейтинг вычисляется по формуле:
\(\displaystyle R=\frac{3S+2C+2F+2Q+D}{50} {\small .}\)
Для удобства вычислений внесем в таблицу обозначения показателей.
По условию следующие показатели отвечают соответственно за:
\(\displaystyle S\) – безопасность,
\(\displaystyle C\) – комфорт,
\(\displaystyle F\) – функциональность,
\(\displaystyle Q\) – качество,
\(\displaystyle D\) – дизайн.
| Модель автомобиля | Безопасность \(\displaystyle S\) | Комфорт \(\displaystyle C\) | Фукциональность \(\displaystyle F\) | Качество \(\displaystyle Q\) | Дизайн \(\displaystyle D\) |
| \(\displaystyle А\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 1\) | \(\displaystyle 4\) | \(\displaystyle 2\) |
| \(\displaystyle Б\) | \(\displaystyle 1\) | \(\displaystyle 1\) | \(\displaystyle 4\) | \(\displaystyle 1\) | \(\displaystyle 5\) |
| \(\displaystyle В\) | \(\displaystyle 3\) | \(\displaystyle 2\) | \(\displaystyle 4\) | \(\displaystyle 1\) | \(\displaystyle 1\) |
Вычислим рейтинги для каждой модели.
\(\displaystyle R=\frac{3S+2C+2F+2Q+D}{50}=\frac{3 \cdot1+2\cdot2+2\cdot1+2\cdot4+2}{50}=\)
\(\displaystyle =\frac{3+4+2+8+2}{50}=\frac{19}{50}=\red{0{,}38} {\small .}\)
Возьмем данные для модели \(\displaystyle А\) и подставим их в формулу для расчёта рейтинга.
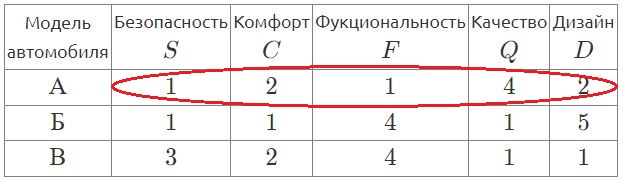
\(\displaystyle S=1{\small ,} \,C=2 {\small ,} \,F=1 {\small ,} \,Q=4{\small ,} \,D =2{\small .}\)
Поэтому
\(\displaystyle R=\frac{3S+2C+2F+2Q+D}{50}=\frac{3 \cdot1+2\cdot2+2\cdot1+2\cdot4+2}{50}=\)
\(\displaystyle =\frac{3+4+2+8+2}{50}=\frac{19}{50}=0{,}38 {\small .}\)
\(\displaystyle R=\frac{3S+2C+2F+2Q+D}{50}=\frac{3 \cdot1+2\cdot1+2\cdot4+2\cdot1+5}{50}=\)
\(\displaystyle =\frac{3+2+8+2+5}{50}=\frac{20}{50}=\red{0{,}4} {\small .}\)
\(\displaystyle R=\frac{3S+2C+2F+2Q+D}{50}=\frac{3 \cdot3+2\cdot2+2\cdot4+2\cdot1+1}{50}=\)
\(\displaystyle =\frac{9+4+8+2+1}{50}=\frac{24}{50}=\red{0{,}48} {\small .}\)
Наибольшим из вычисленных рейтингов является \(\displaystyle R=0{,}48\) для модели \(\displaystyle В {\small .}\) Его и требуется указать в ответе.
Ответ: \(\displaystyle 0{,}48\)