С помощью транспортира найдите, сколько градусов в углах.
\(\displaystyle \angle AOB=\)\(\displaystyle ^{\circ},\) \(\displaystyle \angle DOC=\)\(\displaystyle ^{\circ},\) \(\displaystyle \angle COB=\)\(\displaystyle ^{\circ}\)
Внутренняя шкала разбивает угол на \(\displaystyle 180\) частей справа налево.
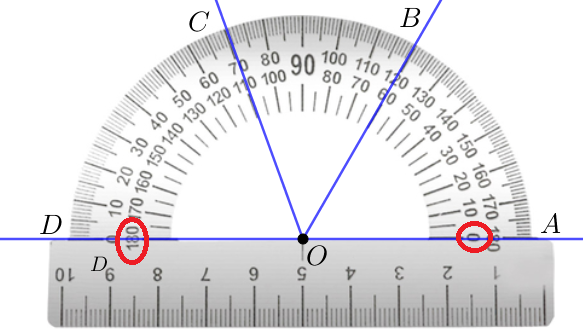
Угол \(\displaystyle AOB\) составляет \(\displaystyle 60\) таких частей, то есть равен \(\displaystyle 60^{\circ}\small.\)
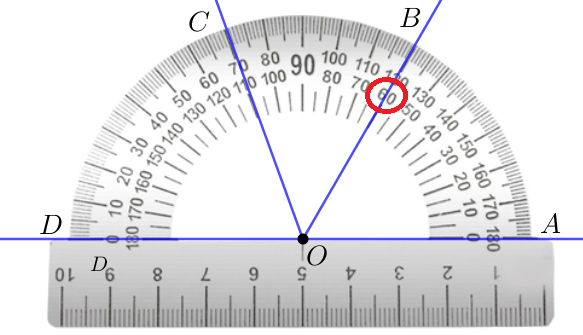
Внешняя шкала разбивает угол на \(\displaystyle 180\) частей слева направо.
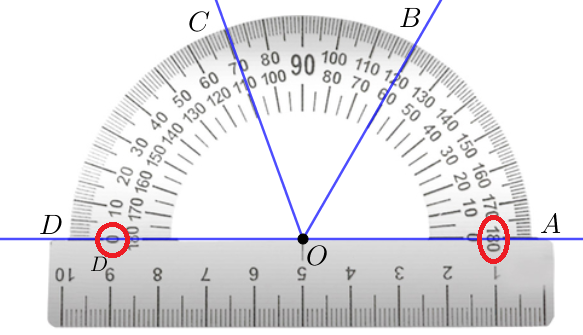
Угол \(\displaystyle DOC\) составляет \(\displaystyle 70\) таких частей, то есть равен \(\displaystyle 70^{\circ}\small.\)
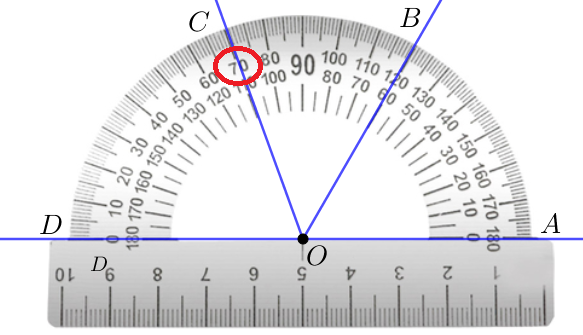
Угол \(\displaystyle COB\) составляет \(\displaystyle 50\) частей по любой шкале. Значит, он равен \(\displaystyle 50^{\circ}\small.\)
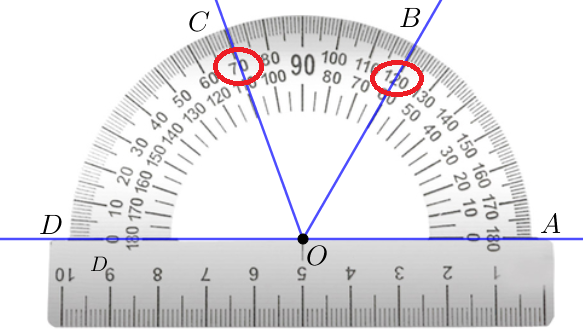 | 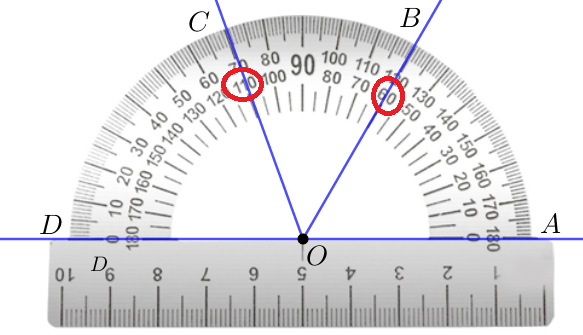 |
| \(\displaystyle 120-70=50\) частей | \(\displaystyle 110-60=50\) частей |