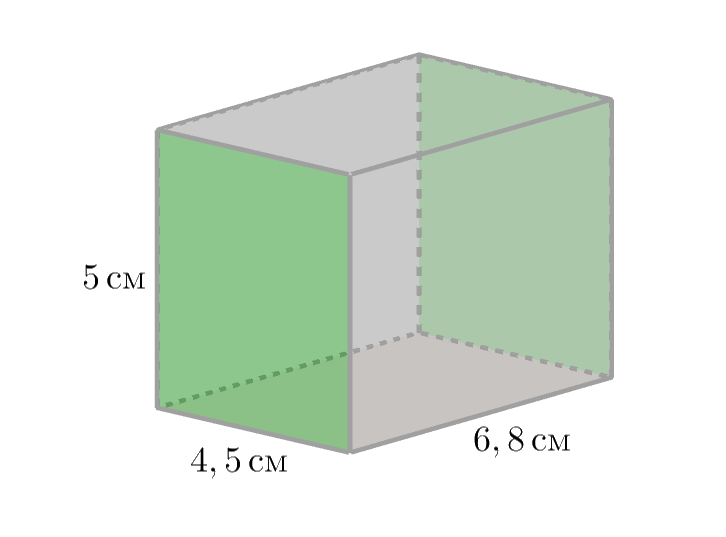
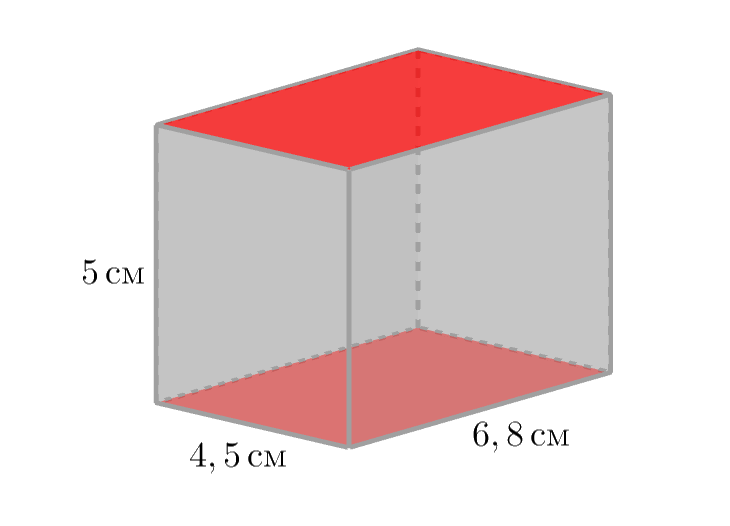
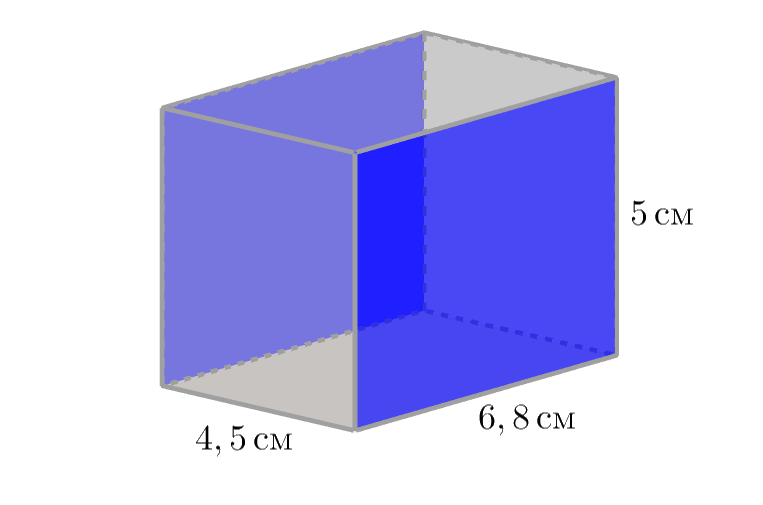
Блок в форме прямоугольного параллелепипеда, измерения которого равны \(\displaystyle 5\)см, \(\displaystyle 4{,}5\)см и \(\displaystyle 6{,}8\)см, необходимо покрасить со всех сторон в один слой. Сколько грамм краски потребуется, если на окраску \(\displaystyle 5\)см2 расходуется \(\displaystyle 4\)г краски?
г.
Чтобы найти, сколько грамм краски потребуется на покраску поверхности блока:
- найдем площадь поверхности блока;
- найдем, сколько грамм краски необходимо на покраску \(\displaystyle 1\)см2;
- найдем, сколько грамм краски понадобится на всю поверхность блока.
1. Площадь поверхности прямоугольного параллелепипеда равна сумме площадей его \(\displaystyle 6\) граней.
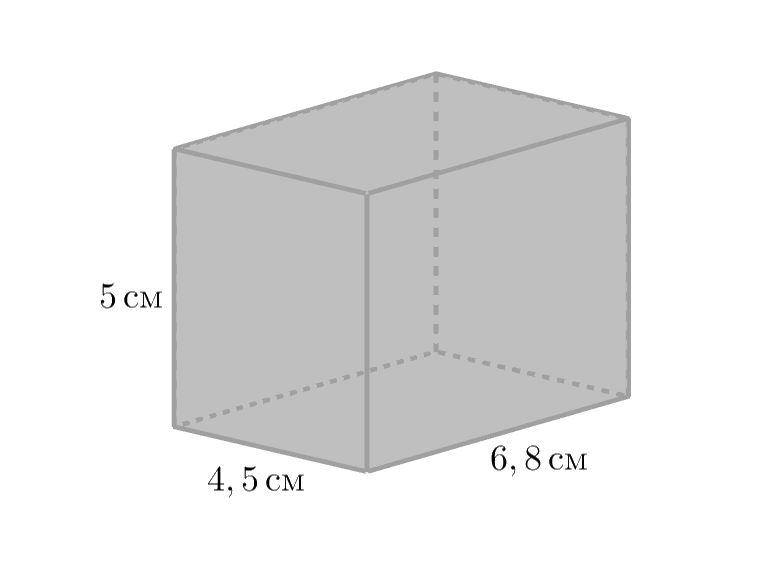
Найдём площади граней параллелепипеда.
\(\displaystyle 5\cdot 4{,}5=22{,}5\)см2.
\(\displaystyle 6{,}8\cdot 4{,}5=30{,}6\)см2.
\(\displaystyle 5\cdot 6{,}8=34\)см2.
Таким образом, площадь поверхности всего параллелепипеда равна:
\(\displaystyle 2\cdot 22{,}5+2\cdot 30{,}6+2\cdot 34= 174{,}2\)см2.
2. Если на \(\displaystyle 5\)см2 необходимо \(\displaystyle 4\)г краски, то на \(\displaystyle 1\)см2, необходимо
\(\displaystyle 4:5=0{,}8\)г.
3. Площадь поверхности всего блока \(\displaystyle 174{,}2\)см2 и на \(\displaystyle 1\)см2 необходимо \(\displaystyle 0{,}8\)г краски.
Тогда на весь блок понадобится
\(\displaystyle 174{,}2\cdot0{,}8=139{,}36\)г.
Ответ: \(\displaystyle 139{,}36\)г.