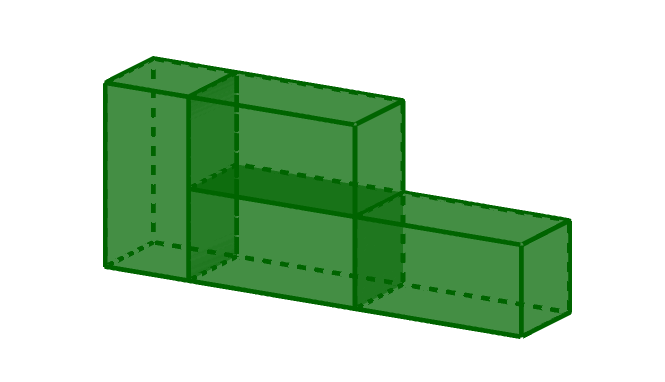
Из блоков длиной \(\displaystyle 15{,}4\)см, шириной \(\displaystyle 7{,}7\)см и высотой \(\displaystyle 7{,}7\)см сложили фигуру, изображённую на рисунке. Найдите площадь поверхности этой фигуры.
см2.
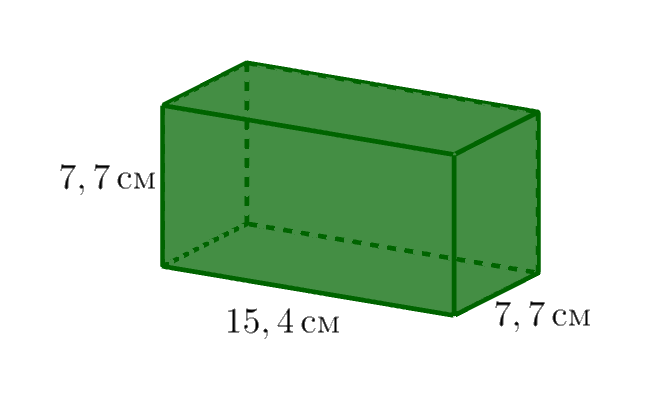
Рассмотрим один блок.
Два измерения у данного параллелепипеда совпадают, поэтому его поверхность состоит из
- четырех прямоугольников со сторонами \(\displaystyle 15{,}4\)см и \(\displaystyle 7{,}7\)см,
- двух квадратов со стороной \(\displaystyle 7{,}7\)см.
Посчитаем количество прямоугольных и количество квадратных граней на поверхности у фигуры, склеенной из блоков.
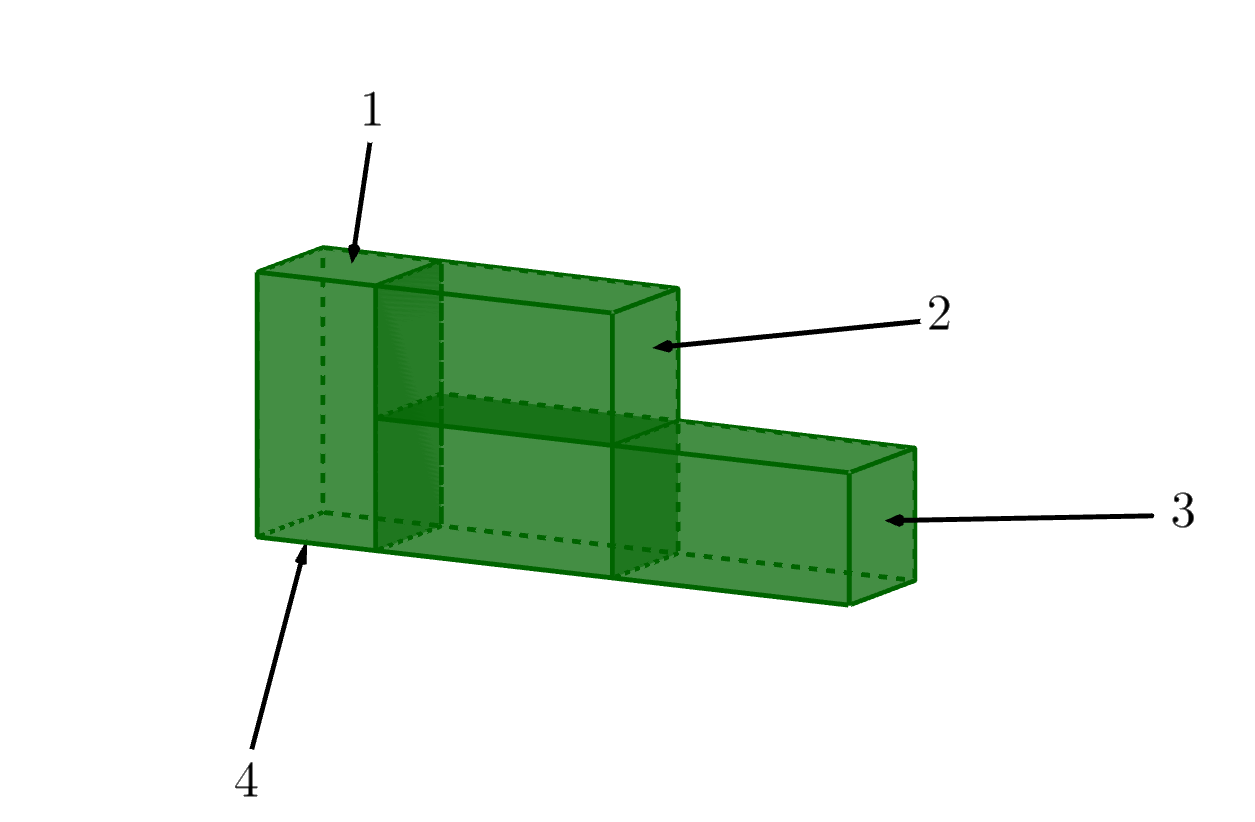
\(\displaystyle 9\) из них обозначены на рисунке. Еще \(\displaystyle 4\) грани расположены так же, как и грани с номерами \(\displaystyle 6\small,\) \(\displaystyle 7\small,\) \(\displaystyle 8\) и \(\displaystyle 9\small,\) но на задней стенке фигуры:
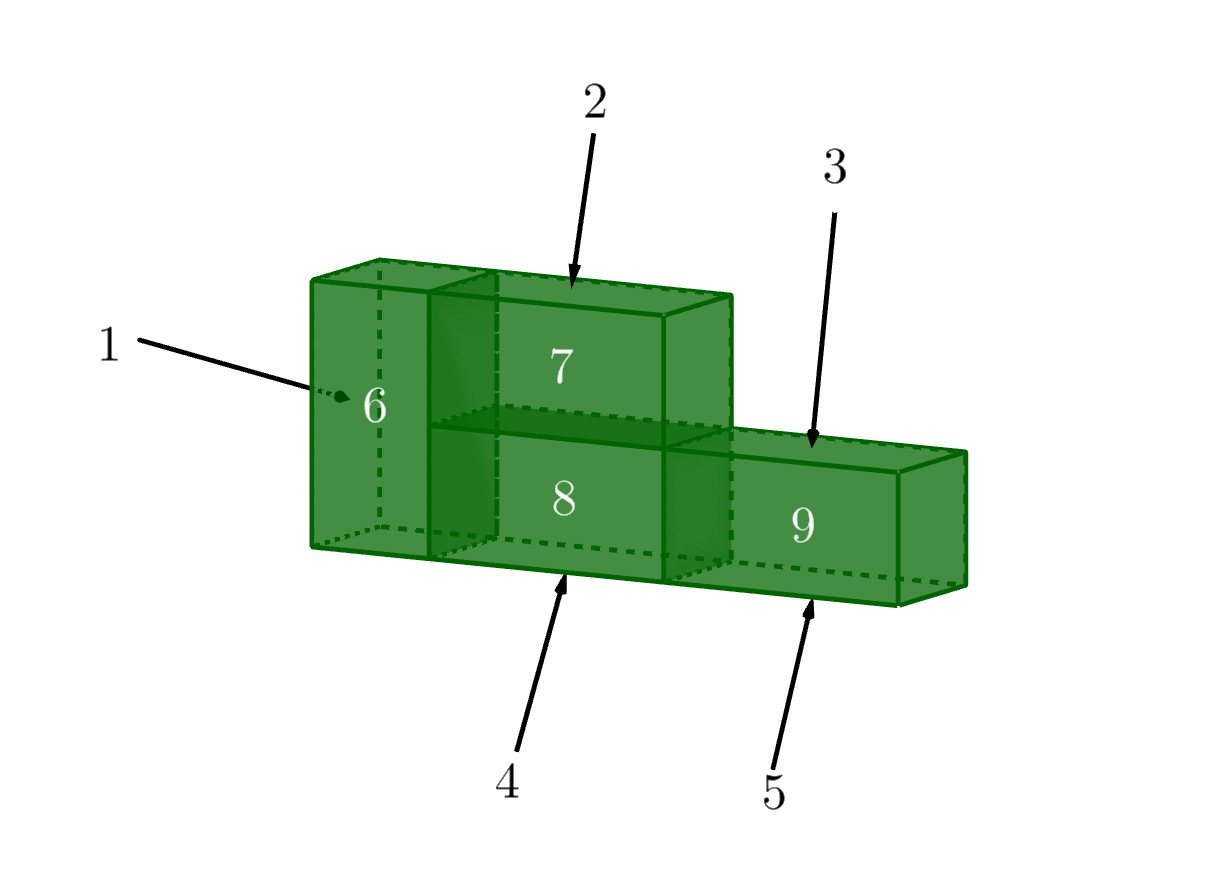
Тогда площадь поверхности всей фигуры, склеенной из блоков, равна сумме четырех площадей квадрата со стороной \(\displaystyle 7{,}7\)см и тринадцати площадей прямоугольника со сторонами \(\displaystyle 15{,}4\)см и \(\displaystyle 7{,}7\)см:
\(\displaystyle \color{red}{S}=\color{blue}{4}\cdot7{,}7\cdot7{,}7+\color{green}{13}\cdot15{,}4\cdot7{,}7=237{,}16+1541{,}54=1778{,}7\)см2.
Ответ: \(\displaystyle 1778{,}7\)см2.