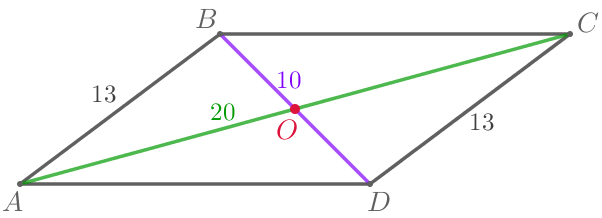
В четырёхугольнике \(\displaystyle ABCD\) \(\displaystyle BC\parallel AD{\small,}\) \(\displaystyle BC=AD{\small,}\) \(\displaystyle AC=20\, {\footnotesize см}{\small,}\) \(\displaystyle BD=10\, {\footnotesize см}{\small,}\) \(\displaystyle AB=13\, {\footnotesize см}{\small.}\) Диагонали четырёхугольника пересекаются в точке \(\displaystyle O{\small.}\) Найдите периметр треугольника \(\displaystyle COD{\small.}\)
\(\displaystyle P_{\triangle COD}=\) \(\displaystyle {\footnotesize см}{\small.}\ \)
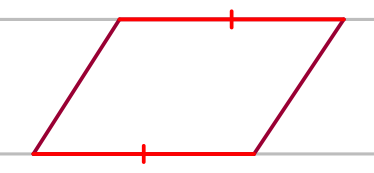
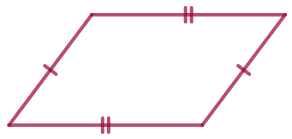
В четырёхугольнике \(\displaystyle ABCD\) две стороны параллельны и равны
\(\displaystyle BC\parallel AD{\small,}\) \(\displaystyle BC= AD{\small.}\)
\(\displaystyle ABCD\) – параллелограмм.
Выполним построение по условию задачи.
\(\displaystyle ABCD\) – параллелограмм:
| 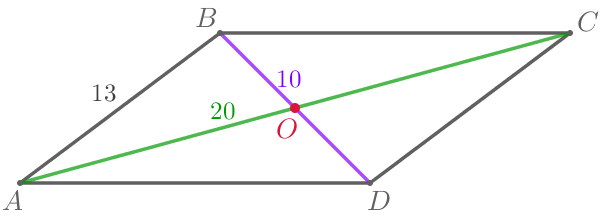 |
Требуется найти периметр треугольника \(\displaystyle COD{\small.}\)
\(\displaystyle P_{\triangle COD}=CD+OC+OD{\small.}\)
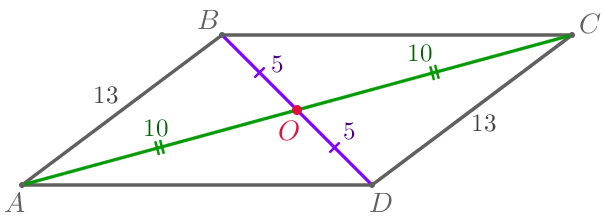
Найдем длины всех сторон треугольника \(\displaystyle COD{\small:}\)
\(\displaystyle CD=13\, {\footnotesize см}{\small.}\)
\(\displaystyle OC=10\, {\footnotesize см}{\small,}\)
\(\displaystyle OD=5\, {\footnotesize см}{\small.}\)
В результате получаем:
\(\displaystyle\begin{aligned}P_{\triangle COD}&=CD+OC+OD=\\&=13+10+5=28\, {\footnotesize см}{\small.}\end{aligned}\)
Ответ: \(\displaystyle P_{\triangle COD}=28\, {\footnotesize см}{\small.}\)