На сторонах \(\displaystyle AB{\small,}\) \(\displaystyle BC{\small,}\) \(\displaystyle CD\) и \(\displaystyle DA\) четырёхугольника \(\displaystyle ABCD\) отмечены соответственно точки \(\displaystyle M{\small,}\) \(\displaystyle N{\small,}\) \(\displaystyle P\) и \(\displaystyle Q\) так, что \(\displaystyle AM=CP{\small,}\) \(\displaystyle BN=DQ{\small,}\) \(\displaystyle BM=DP{\small,}\) \(\displaystyle NC=QA{\small.}\)
Является ли четырёхугольник \(\displaystyle MNPQ\) параллелограммом?
Почему?
По условию задачи выполним чертёж.
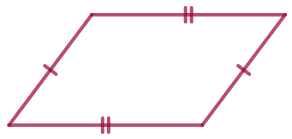
Построим четырёхугольник \(\displaystyle ABCD{\small.}\) На сторонах \(\displaystyle AB{\small,}\) \(\displaystyle BC{\small,}\) \(\displaystyle CD\) и \(\displaystyle DA\) этого четырёхугольника отметим соответственно точки \(\displaystyle M{\small,}\) \(\displaystyle N{\small,}\) \(\displaystyle P\) и \(\displaystyle Q{\small.}\)
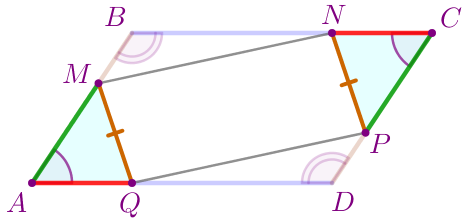
Равные отрезки обозначим одинаковым цветом:
\(\displaystyle \color{green}{AM}=\color{green}{CP}{\small,}\) \(\displaystyle \color{blue}{BN}=\color{blue}{DQ}{\small,}\) \(\displaystyle \color{brown}{BM}=\color{brown}{DP}{\small,}\) \(\displaystyle \color{red}{NC}=\color{red}{QA}{\small.}\) | 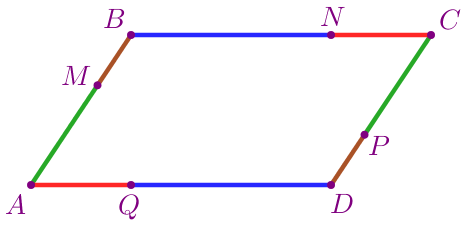 |
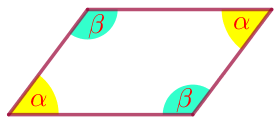
\(\displaystyle ABCD\) – параллелограмм.
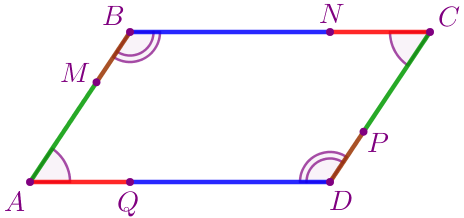 | \(\displaystyle \angle A= \angle C{\small,}\) \(\displaystyle \angle B= \angle D{\small.}\) |
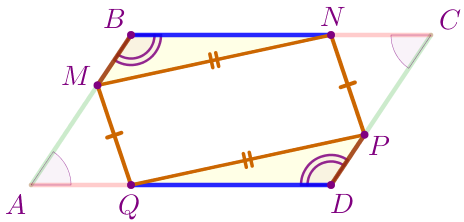
Рассмотрим четырёхугольник \(\displaystyle MNPQ{\small.}\)
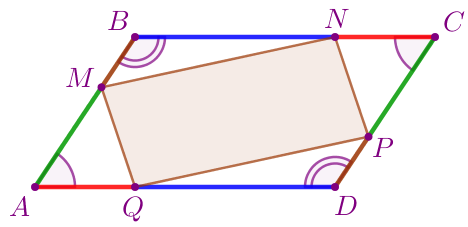
\(\displaystyle MQ=NP{\small.}\)
\(\displaystyle MN=PQ{\small.}\)
В четырёхугольнике \(\displaystyle MNPQ\) противоположные стороны попарно равны. Значит,
\(\displaystyle MNPQ\) – параллелограмм.
| Ответ: | Является ли четырёхугольник \(\displaystyle MNPQ\) параллелограммом? Да. Почему? Противоположные стороны попарно равны. |