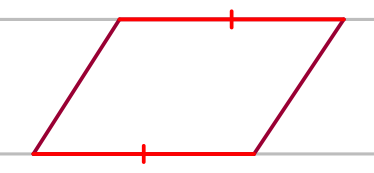
На сторонах \(\displaystyle AB\) и \(\displaystyle CD\) параллелограмма \(\displaystyle ABCD\) отмечены соответственно точки \(\displaystyle T\) и \(\displaystyle K\) так, что \(\displaystyle BT=DK{\small.}\)
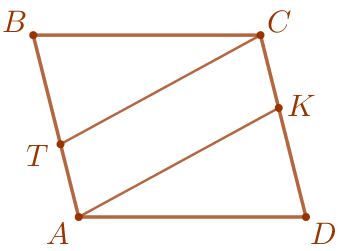
Является ли четырёхугольник \(\displaystyle ATCK\) параллелограммом?
Почему?
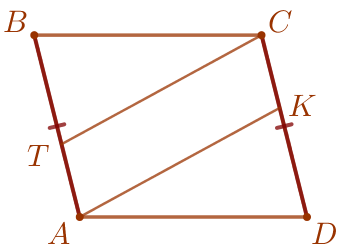 | В параллелограмме противоположные стороны параллельны и равны, то есть \(\displaystyle \color{brown}{AB} \parallel \color{brown}{CD}{\small,}\) \(\displaystyle \color{brown}{AB}=\color{brown}{CD}{\small.}\) |
По условию \(\displaystyle \color{green}{BT}=\color{green}{DK}{\small.}\) Точки \(\displaystyle T\) и \(\displaystyle K\) лежат на отрезках \(\displaystyle \color{brown}{AB}\) и \(\displaystyle \color{brown}{CD}\) соответственно. Тогда \(\displaystyle \color{blue}{AT}=\color{brown}{AB}-\color{green}{BT}{\small,}\) \(\displaystyle \color{blue}{CK}=\color{brown}{CD}-\color{green}{DK}{\small.}\) | 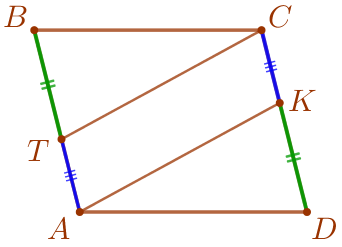 |
Так как разности соответственно равных отрезков равны, то
\(\displaystyle \color{blue}{AT}=\color{blue}{CK}{\small.}\)
Рассмотрим четырёхугольник \(\displaystyle ATCK{\small:}\)
| 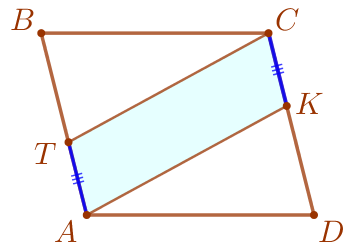 |
Значит, четырёхугольник \(\displaystyle ATCK\) является параллелограммом.
| Ответ: | Является ли четырёхугольник \(\displaystyle ATCK\) параллелограммом? Да. Почему? Противоположные стороны параллельны и равны. |