Точка \(\displaystyle M\) лежит на полуокружности с радиусом \(\displaystyle 1\) и имеет координаты \(\displaystyle (x,\,y){\small:}\)
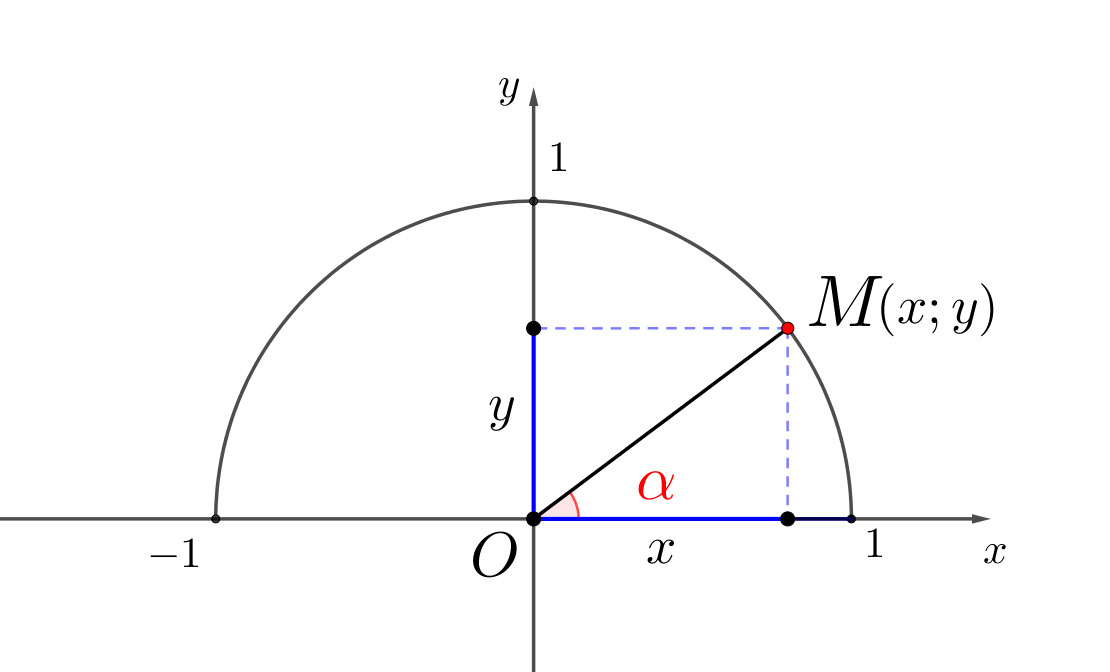
Составьте формулу, по которой вычисляется тангенс угла \(\displaystyle \color{red}{\alpha}{\small:}\)
Четырехугольник \(\displaystyle AMBO\) – прямоугольник.
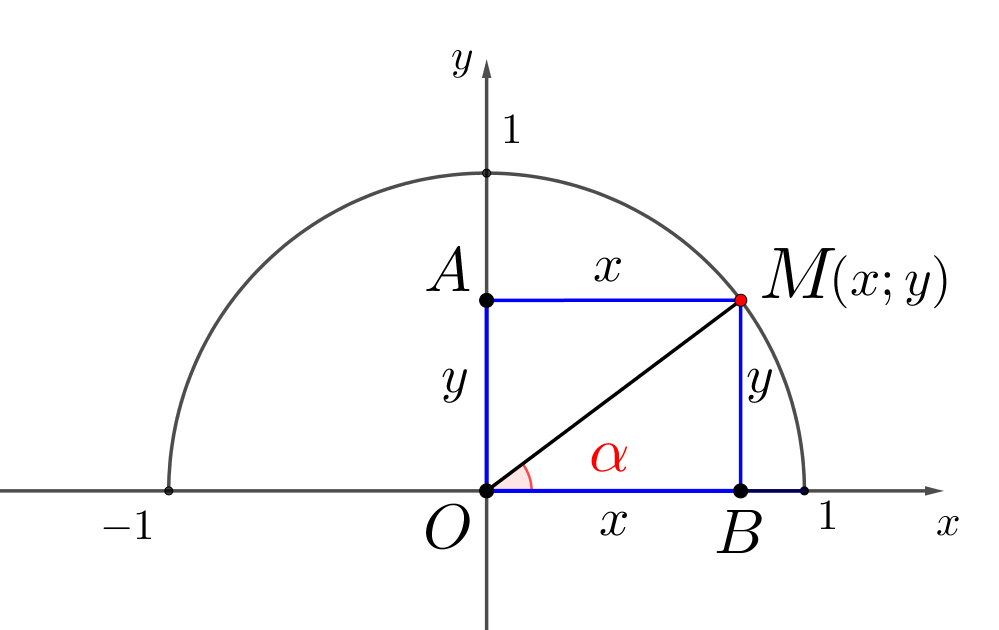
То есть в прямоугольном треугольнике \(\displaystyle OMB{\small:}\) катеты равны \(\displaystyle x\) и \(\displaystyle y\small,\) а гипотенуза \(\displaystyle 1\small.\)
В прямоугольном треугольнике тангенс угла равен отношению противолежащего катета к прилежащему. Получаем:
\(\displaystyle \tg\color{red}{\alpha}=\frac{y}{x}\small.\)
Таким образом, получаем, что если точка \(\displaystyle M\) лежит на единичной окружности, то
\(\displaystyle \tg\color{red}{\alpha}\) равен \(\displaystyle \frac{y}{x}\) – отношению ординаты точки \(\displaystyle M\small\) к её абсциссе.