На рисунке изображена единичная полуокружность. Чему равен тангенс угла \(\displaystyle AOB\small,\) если координаты точки \(\displaystyle B\) равны \(\displaystyle \left( -\frac{5}{13} ;\, \frac{12}{13} \right) \small{?}\)
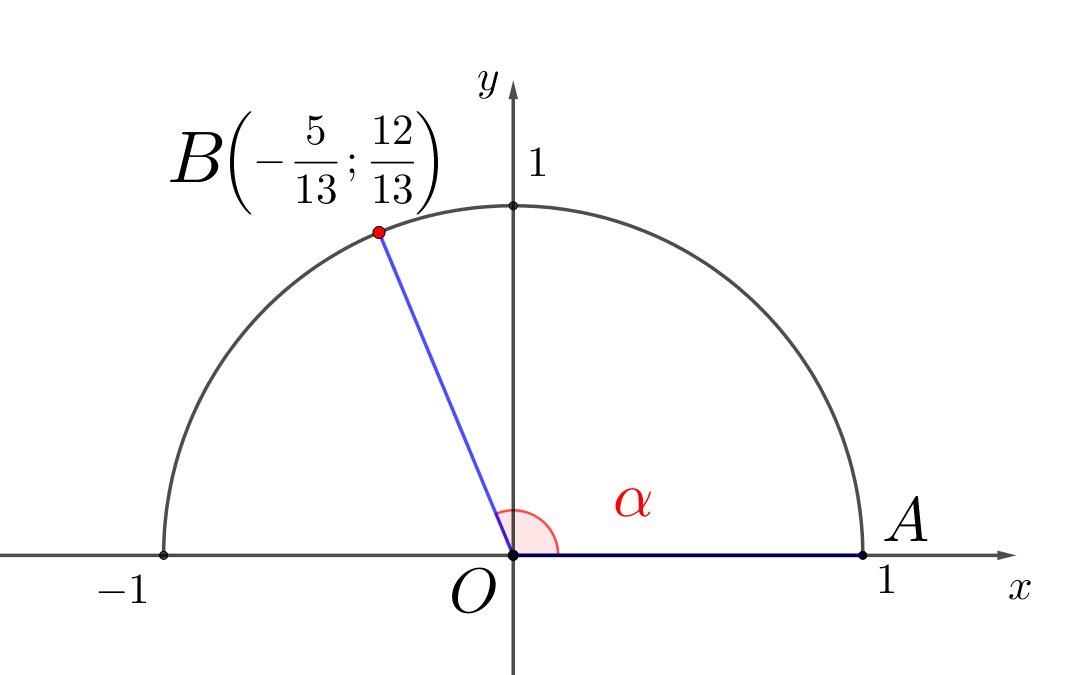
Тангенсом угла \(\displaystyle \color{red}{\alpha}\) ( \(\displaystyle \color{red}{\alpha}\,\cancel{=}\,90^{\circ}\)) называется отношение синуса к косинусу:
\(\displaystyle \tg\color{red}{\alpha}=\frac{\sin\color{red}{\alpha}}{\cos\color{red}{\alpha}}\small.\)
То есть если точка \(\displaystyle M\) лежит на единичной окружности, то
\(\displaystyle \tg\color{red}{\alpha}=\frac{\sin\color{red}{\alpha}}{\cos\color{red}{\alpha}}=\frac{y}{x}\small.\)
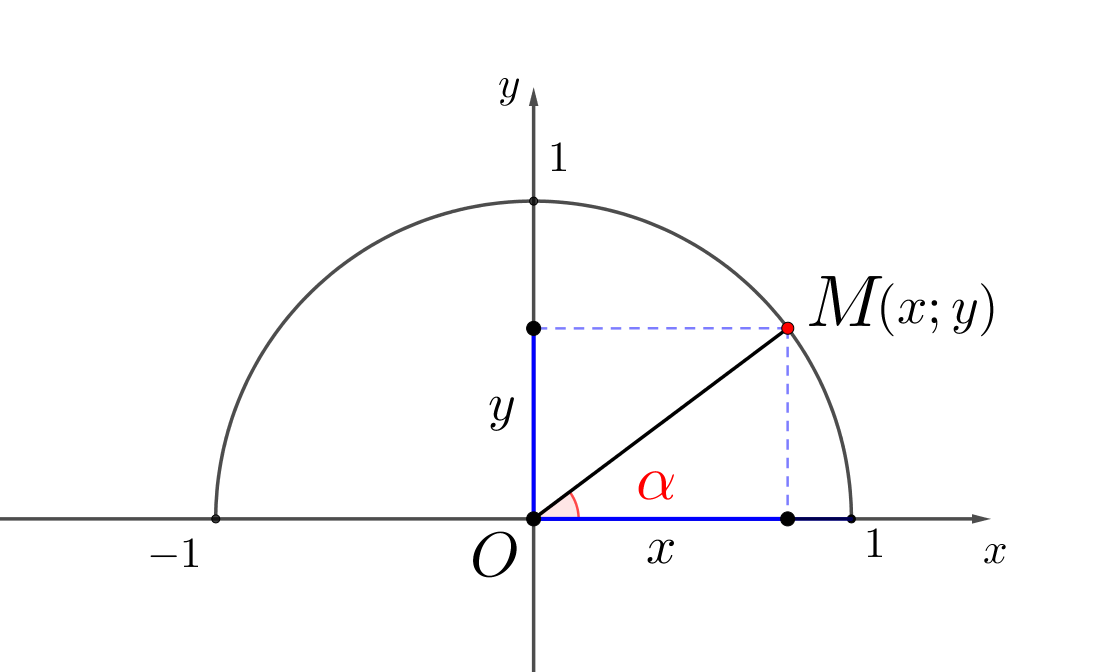
Тогда
\(\displaystyle \tg\angle AOB=\left(\frac{12}{13}\right): \left(-\frac{5}{13}\right)=-\frac{12}{5}\small.\)
Ответ: \(\displaystyle \tg\angle AOB=-\frac{12}{5}\small.\)