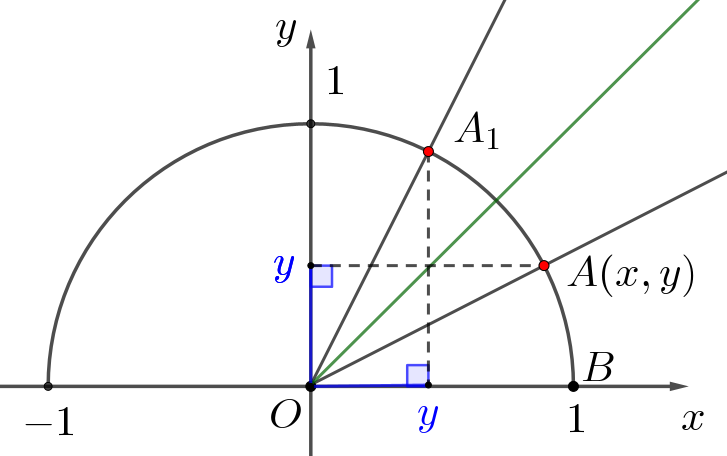
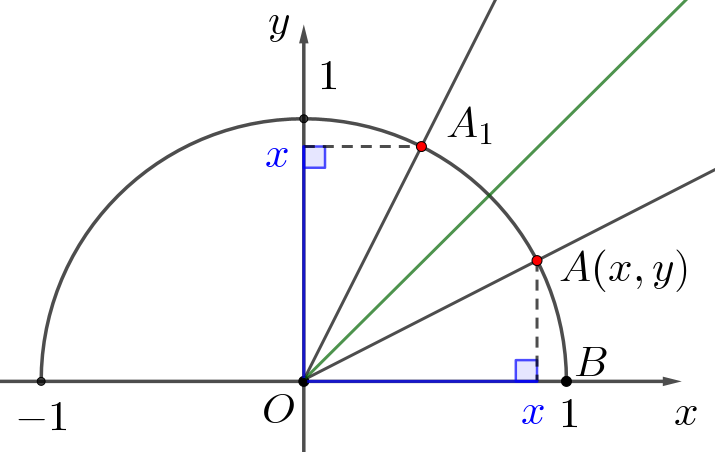
Точку \(\displaystyle A\) отразили относительно биссектрисы угла \(\displaystyle xOy\) и получили точку \(\displaystyle A_1\small.\) При этом точка \(\displaystyle A\) имеет координаты \(\displaystyle (x;\,y)\) и \(\displaystyle \angle AOB=\alpha\small.\)
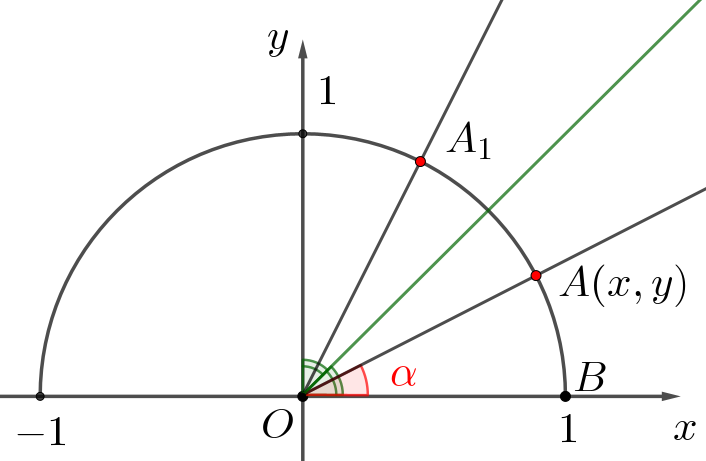
Выразите через \(\displaystyle x\) и \(\displaystyle y\) координаты точки \(\displaystyle A_1{\small:}\)
Найдите \(\displaystyle \angle A_1OB\)
\(\displaystyle \angle A_1OB=\)
и запишите через \(\displaystyle \alpha\) координаты точки \(\displaystyle A_1{\small : } \)
\(\displaystyle A_1=\big(\) \(\displaystyle ;\,\) \(\displaystyle \big)\)
Учитывая, что \(\displaystyle \sin\alpha=y\) и \(\displaystyle \cos\alpha=x\small,\) запишите цепочку равенств:
\(\displaystyle \cos\alpha=x=\)
Точка \(\displaystyle A_1\) симметрична точке \(\displaystyle A\) относительно биссектрисы угла \(\displaystyle xOy\small.\) Тогда:
То есть координаты точки \(\displaystyle A_1{\small:}\)
\(\displaystyle (y;\,x)\small.\)
3. \(\displaystyle \angle xOA=\angle yOA_1{\small.}\)
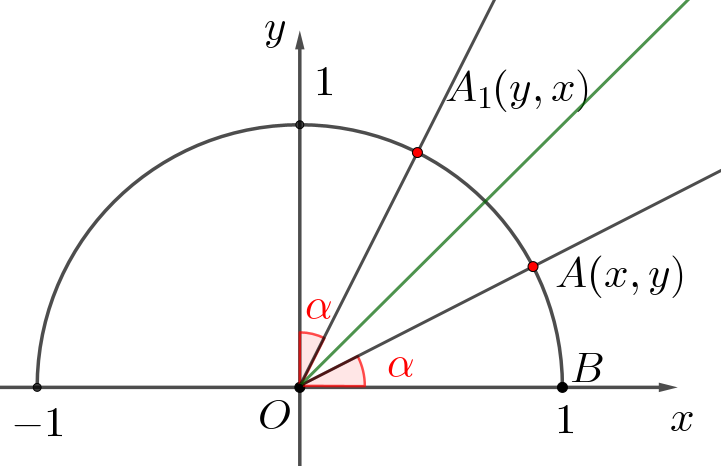
Если \(\displaystyle \angle yOA_1=\alpha\small,\) то \(\displaystyle \angle xOA_1=90^{\circ}-\alpha\small.\) Тогда координаты точки \(\displaystyle A_1\) можно выразить через угол:
точка \(\displaystyle A_1\) имеет координаты \(\displaystyle (\cos(90^{\circ}-\alpha);\,\sin(90^{\circ}-\alpha))\small.\)
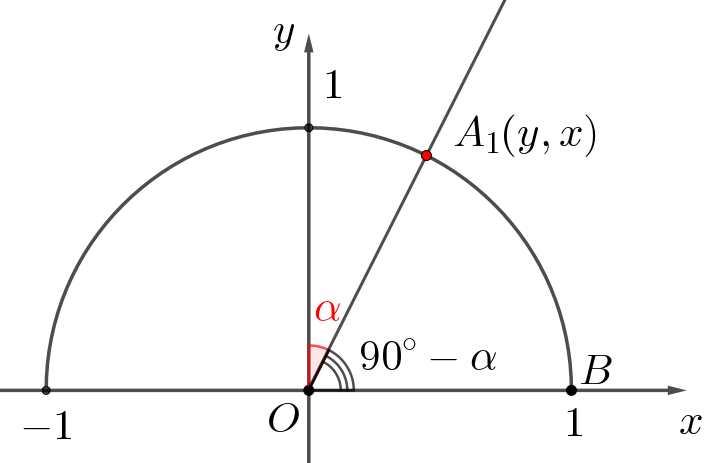
Сопоставляя значения координат точки \(\displaystyle A_1{\small,}\) получаем:
\(\displaystyle \cos(90^{\circ}-\alpha)=y=\sin\alpha\small,\)
\(\displaystyle \sin(90^{\circ}-\alpha)=x=\cos\alpha\small.\)