Опираясь на картинку, заполните таблицу:
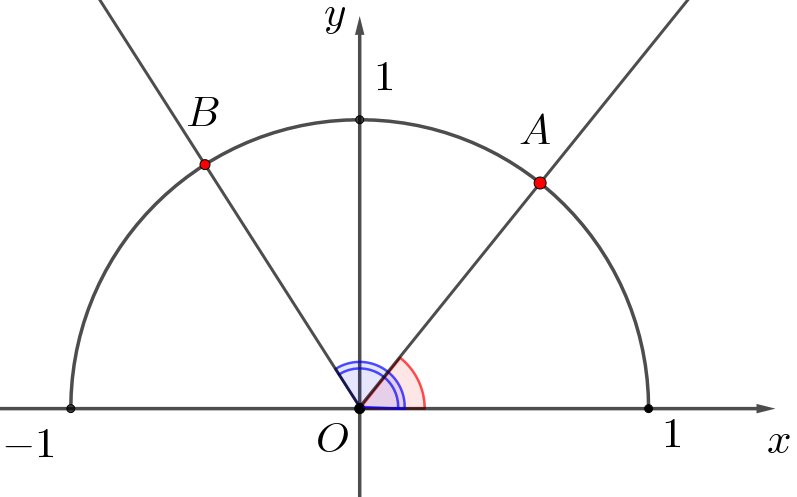
| \(\displaystyle \color{red}{\alpha}\) – острый | \(\displaystyle \color{red}{\alpha}\) – тупой | |
| \(\displaystyle \sin\color{red}{\alpha}\) | ||
| \(\displaystyle \cos\color{red}{\alpha}\) |
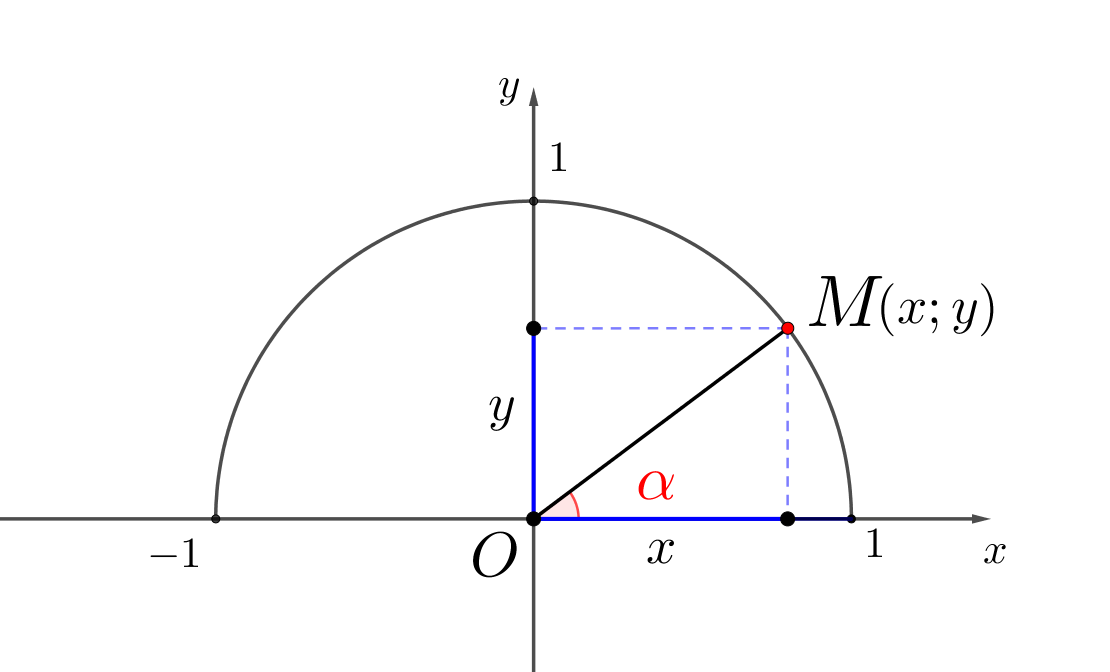
Точка \(\displaystyle M\) лежит на единичной полуокружности. Тогда для любого угла \(\displaystyle \color{red}{\alpha}\) из промежутка \(\displaystyle 0^{\circ}\leqslant\color{red}{\alpha}\leqslant180^{\circ}{\small:}\)
- косинусом угла \(\displaystyle \color{red}{\alpha}\) называется абсцисса точки \(\displaystyle M\small,\)
- синусом угла \(\displaystyle \color{red}{\alpha}\) называется ордината точки \(\displaystyle M\small.\)
Если \(\displaystyle \color{red}{\alpha}\) острый, то
\(\displaystyle \cos\color{red}{\alpha}>0\) и \(\displaystyle \sin\color{red}{\alpha}>0\small.\)
Угол \(\displaystyle \color{red}{\alpha}\) острый, если для него верно \(\displaystyle 0^{\circ}<\color{red}{\alpha}<90^{\circ}\small.\) Тогда точка, соответствующая \(\displaystyle \color{red}{\alpha}\small,\) лежит на красной дуге:
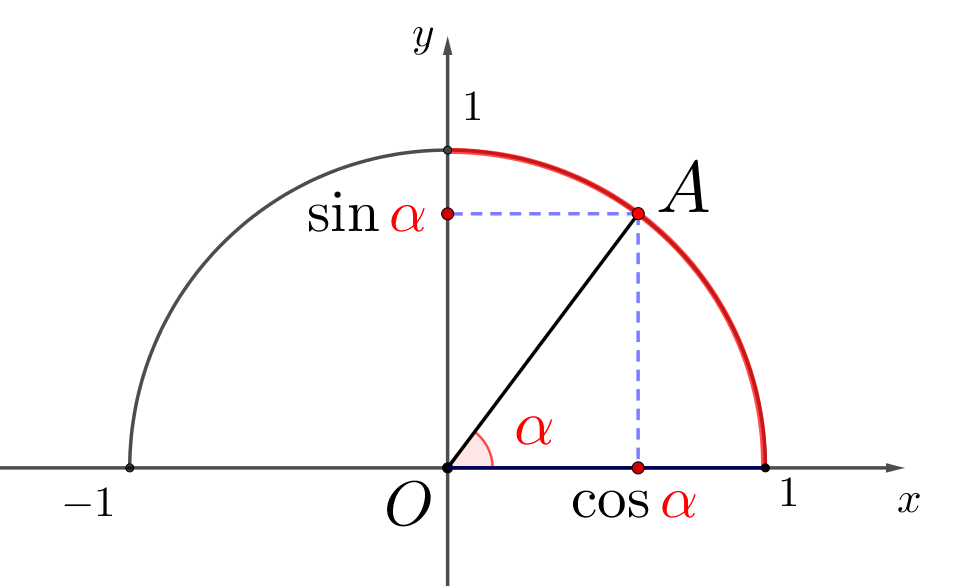
Точки на красной дуге имеют положительную абсциссу и ординату.
Значит, если \(\displaystyle \color{red}{\alpha}\) острый, то
\(\displaystyle \cos\color{red}{\alpha}>0\) и \(\displaystyle \sin\color{red}{\alpha}>0\small.\)
Если \(\displaystyle \color{red}{\alpha}\) тупой, то
\(\displaystyle \cos\color{red}{\alpha}<0\) и \(\displaystyle \sin\color{red}{\alpha}>0\small.\)
Угол \(\displaystyle \color{red}{\alpha}\) тупой, если для него верно \(\displaystyle 90^{\circ}<\color{red}{\alpha}<180^{\circ}\small.\) Тогда точка, соответствующая \(\displaystyle \color{red}{\alpha}\small,\) лежит на синей дуге:
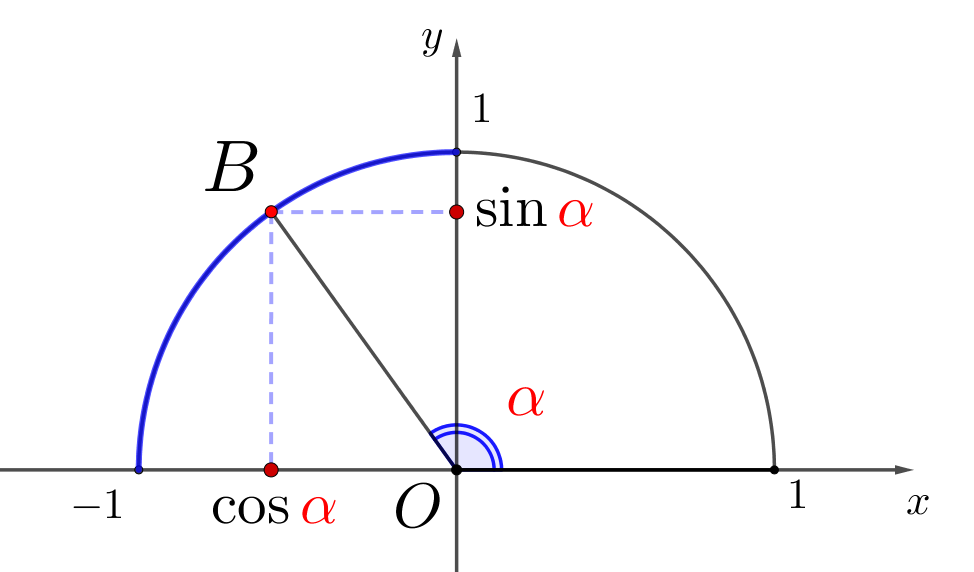
Точки на синей дуге имеют отрицательную абсциссу и положительную ординату.
Значит, если \(\displaystyle \color{red}{\alpha}\) тупой, то
\(\displaystyle \cos\color{red}{\alpha}<0\) и \(\displaystyle \sin\color{red}{\alpha}>0\small.\)