В параллелограмме \(\displaystyle MNPQ\) проведён перпендикуляр \(\displaystyle NH\) к прямой \(\displaystyle MQ{\small,}\) причем точка \(\displaystyle H\) лежит на стороне \(\displaystyle MQ{\small.}\) Найдите стороны параллелограмма, если известно, что \(\displaystyle MH=5 \, {\footnotesize см}{\small,}\) \(\displaystyle HQ=8 \, {\footnotesize см}{\small,}\) \(\displaystyle \angle MNH=30^{\circ}{\small.}\)
\(\displaystyle {\footnotesize см}{\small;}\) \(\displaystyle {\footnotesize см}{\small;}\) \(\displaystyle {\footnotesize см}{\small;}\) \(\displaystyle {\footnotesize см}{\small.}\)
По условию задачи выполним построение.
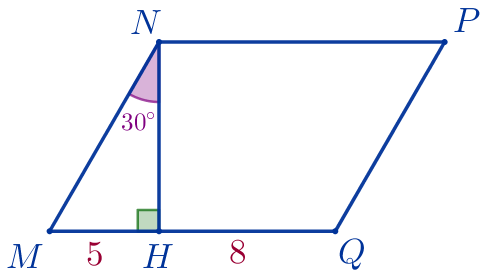 | \(\displaystyle MNPQ\) – параллелограмм:
|
Требуется найти стороны параллелограмма \(\displaystyle MNPQ{\small.}\)
Свойство параллелограмма
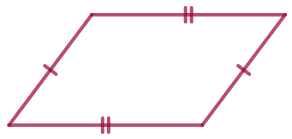 | Противоположные стороны параллелограмма попарно равны. |
Найдём стороны \(\displaystyle MQ\) и \(\displaystyle NP{\small.}\)
Точка \(\displaystyle H\) лежит на стороне \(\displaystyle MQ{\small:}\)
Тогда \(\displaystyle\begin{aligned}MQ&=MH+HQ=\\&=5+8=13\, \footnotesize см {\small.}\end{aligned}\) | 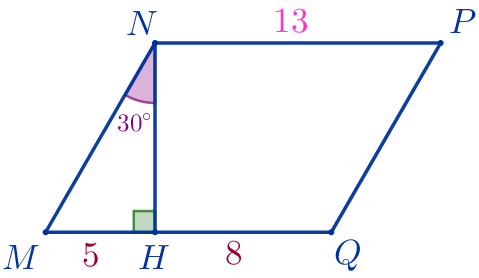 |
\(\displaystyle NP\) и \(\displaystyle MQ\) – противоположные стороны параллелограмма \(\displaystyle MNPQ{\small,}\) значит,
\(\displaystyle NP=MQ=13\, \footnotesize см {\small.}\)
Найдём стороны \(\displaystyle MN\) и \(\displaystyle PQ{\small.}\)
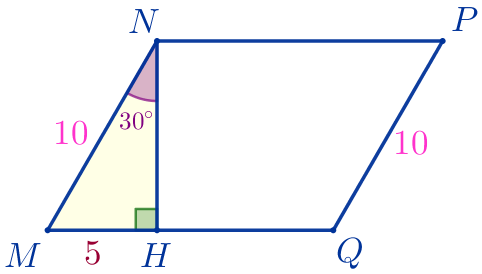
Рассмотрим треугольник \(\displaystyle MNH{\small:}\)
 |
|
В прямоугольном треугольнике напротив угла \(\displaystyle 30^{\circ}\) лежит катет равный половине гипотенузы.
То есть
\(\displaystyle MN=2\cdot MH=2 \cdot 5=10\, {\footnotesize см}{\small.}\)
\(\displaystyle PQ\) и \(\displaystyle MN\) – противоположные стороны параллелограмма \(\displaystyle MNPQ{\small,}\) значит,
\(\displaystyle PQ=MN=10\, \footnotesize см {\small.}\)
Таким образом, стороны параллелограмма \(\displaystyle MNPQ\) равны:
\(\displaystyle MN=PQ=10\, {\footnotesize см}{\small;}\)
\(\displaystyle MQ=NP=13\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle 10\, {\footnotesize см}{\small;}\) \(\displaystyle 13\, {\footnotesize см}{\small;}\) \(\displaystyle 10\, {\footnotesize см}{\small;}\) \(\displaystyle 13\, {\footnotesize см}{\small.}\)