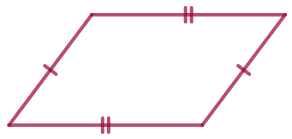
Периметр параллелограмма \(\displaystyle ABCD\) равен \(\displaystyle 50\, \footnotesize см {\small,}\) \(\displaystyle \angle C=30^{\circ}{\small,}\) а перпендикуляр \(\displaystyle BH\) к прямой \(\displaystyle CD\) равен \(\displaystyle 6{,}5\, \footnotesize см {\small.}\) Найдите стороны параллелограмма.
\(\displaystyle \footnotesize см {\small;}\) \(\displaystyle \footnotesize см {\small;}\) \(\displaystyle \footnotesize см {\small;}\) \(\displaystyle \footnotesize см {\small.}\)
По условию задачи выполним построение.
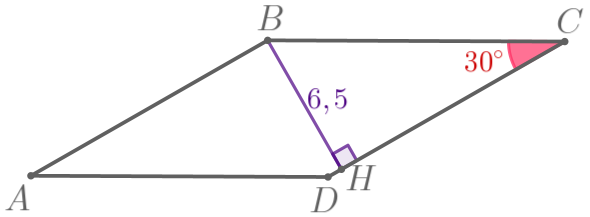 | \(\displaystyle ABCD\) – параллелограмм:
|
Требуется найти стороны параллелограмма \(\displaystyle ABCD{\small.}\)
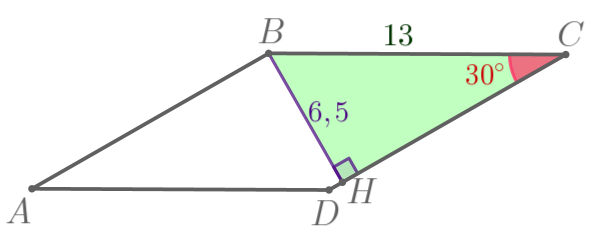
Рассмотрим треугольник \(\displaystyle BCH{\small:}\)
 |
|
В прямоугольном треугольнике напротив угла \(\displaystyle 30^{\circ}\) лежит катет равный половине гипотенузы.
Значит,
\(\displaystyle BC=2\cdot BH=2 \cdot 6{,}5=13\, {\footnotesize см}{\small.}\)
\(\displaystyle AD=BC=13\, {\footnotesize см}{\small;}\) \(\displaystyle AB=CD=x\, {\footnotesize см}{\small.}\) | 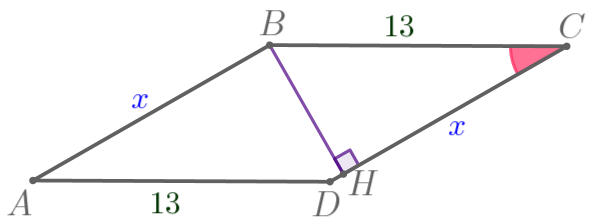 |
Известно, что периметр параллелограмма \(\displaystyle ABCD\) равен \(\displaystyle 50\, \footnotesize см {\small.}\) То есть
\(\displaystyle P_{ABCD}=2(AB+AD)=50\, \footnotesize см {\small.}\)
Значит,
\(\displaystyle AB+AD=25\, \footnotesize см {\small.}\)
Подставим \(\displaystyle AD=13\, {\footnotesize см}{\small:}\)
\(\displaystyle AB+13=25\, \footnotesize см {\small;}\)
\(\displaystyle AB=25-13=12\, \footnotesize см {\small.}\)
Таким образом, стороны параллелограмма \(\displaystyle ABCD\) равны:
\(\displaystyle AD=BC=13\, {\footnotesize см}{\small;}\)
\(\displaystyle AB=CD=12\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle 12\, {\footnotesize см}{\small;}\) \(\displaystyle 13\, {\footnotesize см}{\small;}\) \(\displaystyle 12\, {\footnotesize см}{\small;}\) \(\displaystyle 13\, {\footnotesize см}{\small.}\)