На картинке изображен треугольник, обозначены его стороны и один из углов.
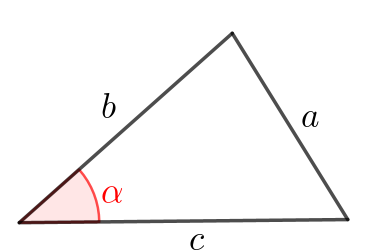
Напишите формулу, по которой можно найти косинус \(\displaystyle \alpha\small,\) зная \(\displaystyle a,\,b\) и \(\displaystyle c{\small:}\)
Используя формулу, найдите \(\displaystyle \cos\alpha\small,\) если \(\displaystyle a=8,\,b=11\) и \(\displaystyle c=12{\small:}\)
Воспользуемся теоремой косинусов:
Теорема косинусов
В треугольнике один из углов \(\displaystyle \color{red}\alpha\small,\) две прилежащие к этому углу стороны равны \(\displaystyle b\) и \(\displaystyle c\small.\) Тогда квадрат третьей стороны \(\displaystyle a\) вычисляется по формуле:
\(\displaystyle a^2=b^2+c^2-2bc\cos \color{red}\alpha\small.\)
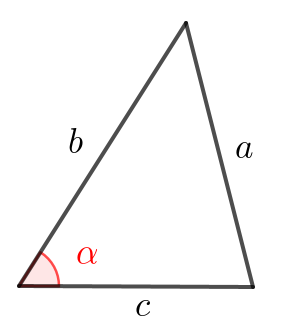
Преобразуем формулу, чтобы выразить \(\displaystyle \cos \alpha\) через \(\displaystyle a,\,b\) и \(\displaystyle c{\small.}\)
Перенесем слагаемое с косинусом влево, а все остальное вправо:
\(\displaystyle 2bc\cos \color{red}\alpha=b^2+c^2-a^2\small.\)
Поделим обе части на \(\displaystyle 2bc{\small:}\)
\(\displaystyle \cos \color{red}\alpha=\frac{b^2+c^2-a^2}{2bc}\small.\)
Подставим в формулу известные значения \(\displaystyle a=8,\,b=11\) и \(\displaystyle c=12{\small:}\)
\(\displaystyle \cos \color{red}\alpha=\frac{b^2+c^2-a^2}{2bc}=\frac{11^2+12^2-8^2}{2\cdot11\cdot12}=\frac{67}{88}\small.\)