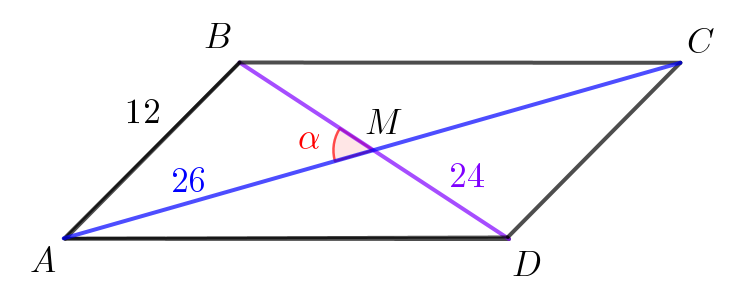
В параллелограмме сторона равна \(\displaystyle 12\small,\) а диагонали равны \(\displaystyle 24\) и \(\displaystyle 26\small.\) Найдите косинус острого угла между диагоналями.
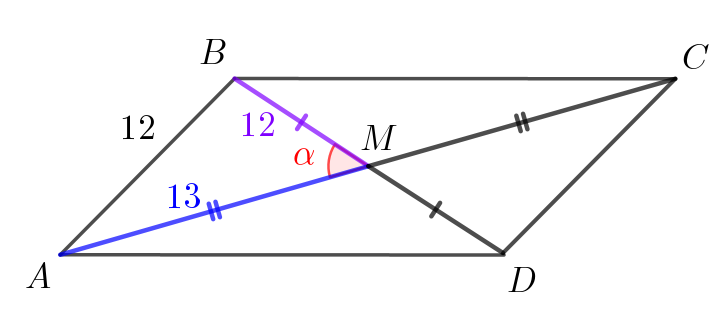
В параллелограмме диагонали точкой пересечения делятся пополам. То есть \(\displaystyle AM=\frac{AC}{2}=\frac{26}{2}=13\) и \(\displaystyle BM=\frac{BD}{2}=\frac{24}{2}=12\small.\) |
|
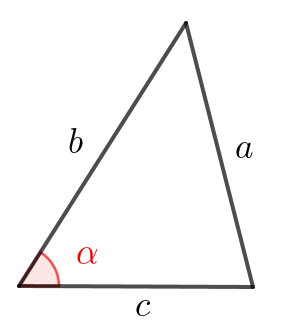
Напишем теорему косинусов для треугольника\(\displaystyle ABM{\small:}\)
\(\displaystyle AB^2=AM^2+BM^2-2\cdot AM\cdot BM\cdot\cos\color{red}{\alpha}\small.\)
Подставим \(\displaystyle AB=12,\, AM=13\) и \(\displaystyle BM=12\) и найдем \(\displaystyle \cos\color{red}{\alpha}{\small:}\)
\(\displaystyle 12^2=13^2+12^2-2\cdot13\cdot12\cdot\cos\color{red}{\alpha}\small,\)
\(\displaystyle 2\cdot13\cdot12\cdot\cos\color{red}{\alpha}=169\small,\)
\(\displaystyle \cos\color{red}{\alpha}=\frac{169}{2\cdot13\cdot12}=\frac{13}{24}\small.\)
Косинус положительный у острых углов, а у тупых – отрицательный. Тогда \(\displaystyle \color{red}{\alpha}\, - \) необходимый острый угол.
Ответ: \(\displaystyle \cos\color{red}{\alpha}=\frac{13}{24}\small.\)