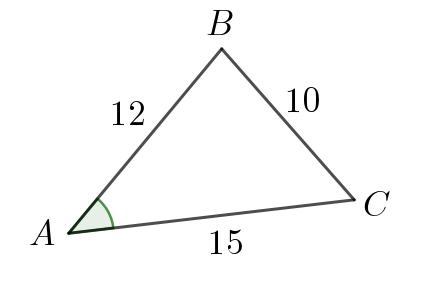
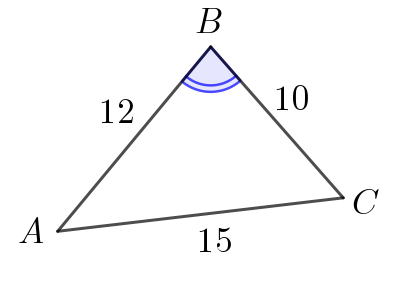
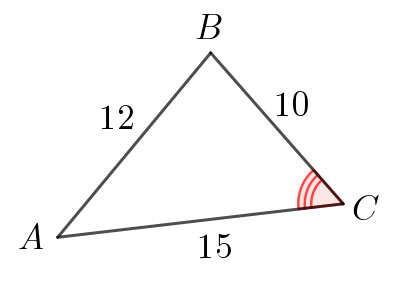
Стороны треугольника равны \(\displaystyle 10,\,12,\,15\small.\) Найдите косинусы углов этого треугольника.

Косинусы углов равны:
- \(\displaystyle \cos\angle A=\)
- \(\displaystyle \cos\angle B=\)
- \(\displaystyle \cos\angle C=\)
\(\displaystyle \cos\angle A=\frac{269}{360}\small.\)
Запишем теорему косинусов для стороны \(\displaystyle BC\small,\) противолежащей углу \(\displaystyle A{\small:}\) \(\displaystyle BC^2=AB^2+AC^2-2\cdot AB\cdot AC\cdot\cos\angle A\small.\) Подставим известные значения сторон и найдем \(\displaystyle \cos\angle A{\small:}\) \(\displaystyle 10^2=12^2+15^2-2\cdot12\cdot15\cdot\cos\angle A\small,\) \(\displaystyle 100=369-360\cos\angle A\small,\) \(\displaystyle 360\cos\angle A=369-100\small,\) \(\displaystyle \cos\angle A=\frac{269}{360}\small.\) |
|
\(\displaystyle \cos\angle B=\frac{19}{240}\small.\)
\(\displaystyle \cos\angle C=\frac{181}{300}\small.\)