Две стороны треугольника равны \(\displaystyle 3\) и \(\displaystyle 4\small,\) а угол между этими сторонами равен \(\displaystyle 60^{\circ}\small.\) Решите этот треугольник.
(Найдите все стороны и углы треугольника.)
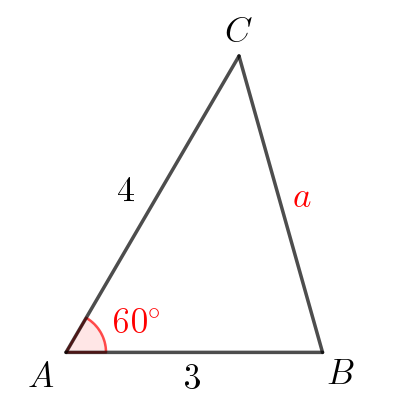
- \(\displaystyle BC=\)
- \(\displaystyle \cos\angle B=\)
- \(\displaystyle \cos\angle C=\)
Используя теорему косинусов, найдем все элементы треугольника.
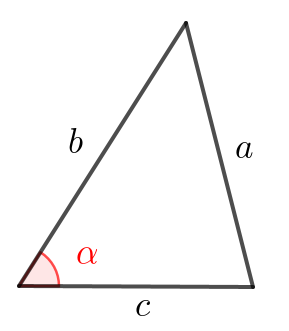
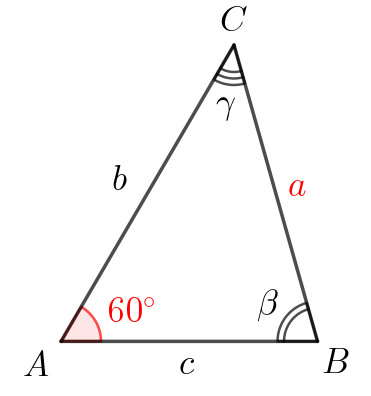
Для удобства обозначим стороны и углы треугольника, как показано на рисунке. При этом:
|
|
\(\displaystyle a=\sqrt{13}\small.\)
По теореме косинусов:
\(\displaystyle a^2=b^2+c^2-2 bc\cos \alpha\small.\)
Подставим известные значения: \(\displaystyle b=4\small,\) \(\displaystyle c=3\) и \(\displaystyle \cos\alpha=\cos60^{\circ}=\frac{1}{2}\small.\) Получаем:
\(\displaystyle a^2=4^2+3^2-2\cdot4\cdot3\cdot\frac{1}{2}=13\small,\)
\(\displaystyle a=\sqrt{13}\small.\)
Теперь, зная все стороны, найдем углы.
\(\displaystyle \cos\gamma=\frac{5}{2\sqrt{13}}\small.\)
Получаем:
\(\displaystyle c^2=b^2+a^2-2 b a\cos \gamma\small.\)
Подставим известные длины сторон и найдем \(\displaystyle \cos \gamma\small:\)
\(\displaystyle 3^2=4^2+(\sqrt{13})^2-2\cdot4\cdot\sqrt{13}\cdot\cos \gamma\small,\)
\(\displaystyle 2\cdot4\cdot\sqrt{13}\cdot\cos \gamma=4^2+(\sqrt{13})^2-3^2\small,\)
\(\displaystyle 8\sqrt{13}\cos \gamma=20\small,\)
\(\displaystyle \cos \gamma=\frac{5}{2\sqrt{13}}\small.\)
\(\displaystyle \cos\beta=\frac{1}{\sqrt{13}}\small.\)