На единичной окружности отмечена точка \(\displaystyle A\small,\) ее координаты равны \(\displaystyle (0{,}6;\,0{,}8)\small.\) Точку \(\displaystyle A\) отразили относительно биссектрисы угла \(\displaystyle xOy\) и получили точку \(\displaystyle A_1{\small:}\)
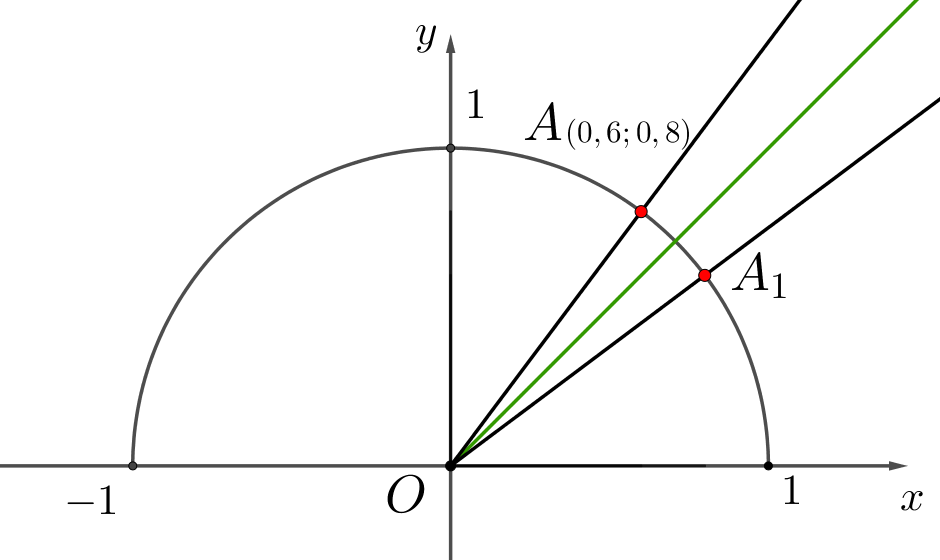
Чему равны координаты точки \(\displaystyle A_1?\)
Точка \(\displaystyle A_1\) симметрична точке \(\displaystyle A\) относительно биссектрисы угла \(\displaystyle xOy\small.\) Тогда:
Проведем перпендикуляры \(\displaystyle AM\) и \(\displaystyle A_1N{\small:}\)
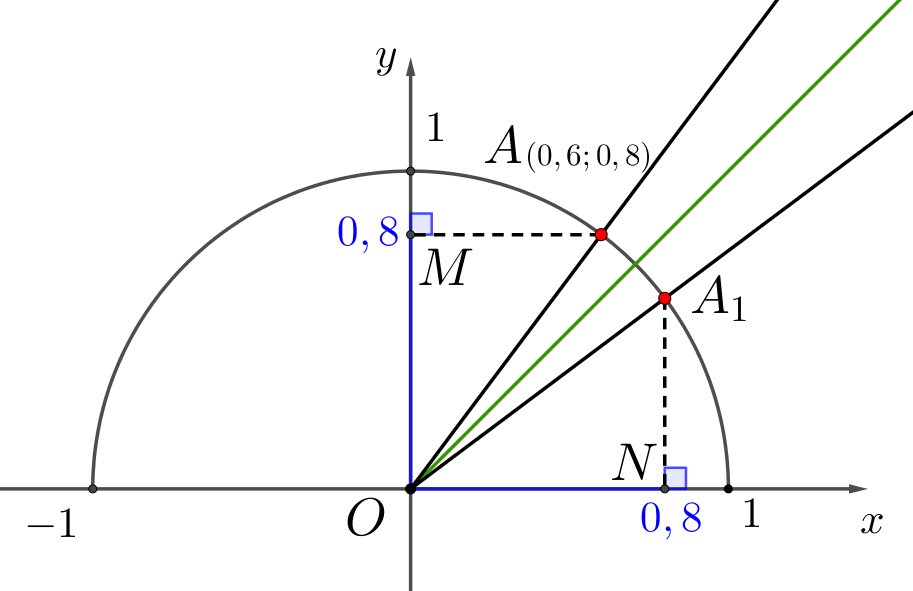
Картинка симметрична относительно биссектрисы угла \(\displaystyle xOy\small.\)
Тогда абсцисса \(\displaystyle A_1\) – отрезок \(\displaystyle ON\) равна ординате \(\displaystyle A\) – отрезку \(\displaystyle OM{\small:}\)
\(\displaystyle OM=ON=0{,}8\small.\)
Проведем перпендикуляры \(\displaystyle AK\) и \(\displaystyle A_1L{\small:}\)
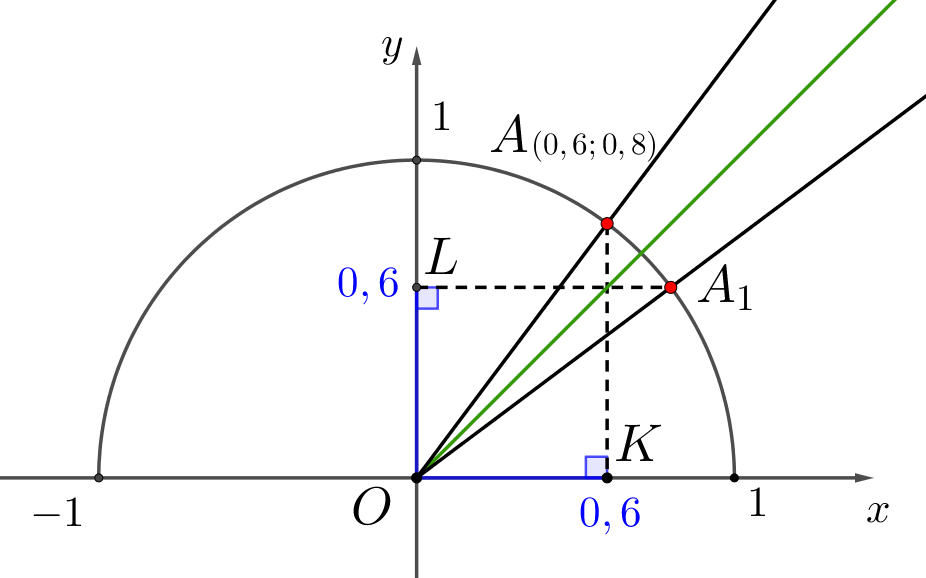
Картинка симметрична относительно биссектрисы угла \(\displaystyle xOy\small.\)
Тогда ордината \(\displaystyle A_1\) – отрезок \(\displaystyle OL\) равна абсциссе \(\displaystyle A\) – отрезку \(\displaystyle OK{\small:}\)
\(\displaystyle OL=OK=0{,}6\small.\)
То есть координаты точки \(\displaystyle A_1{\small:}\)
\(\displaystyle (0{,}8;\,0{,}6)\small.\)