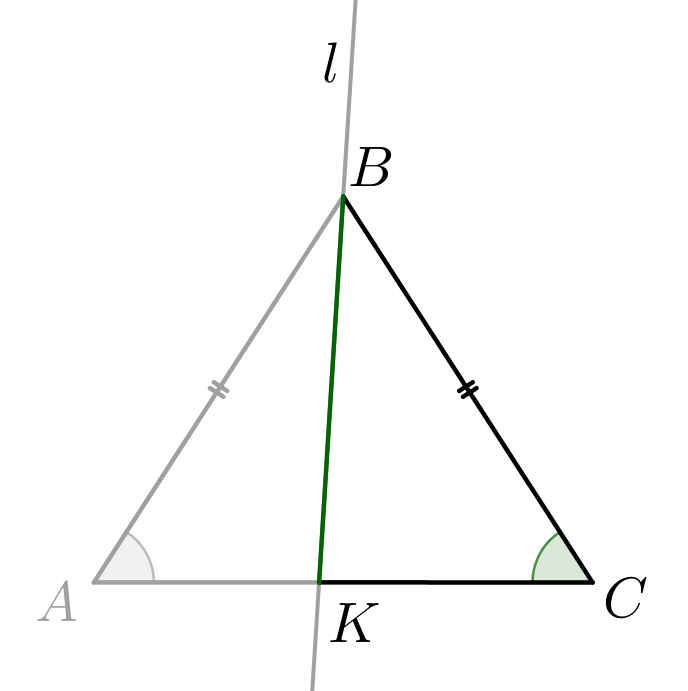
Прямая \(\displaystyle l\) проходит через вершину равнобедренного треугольника и делит его основание в отношении \(\displaystyle 14:17\small.\) Найдите, чему равно отношение радиусов окружностей, описанных около треугольников, на которые прямая делит равнобедренный треугольник.
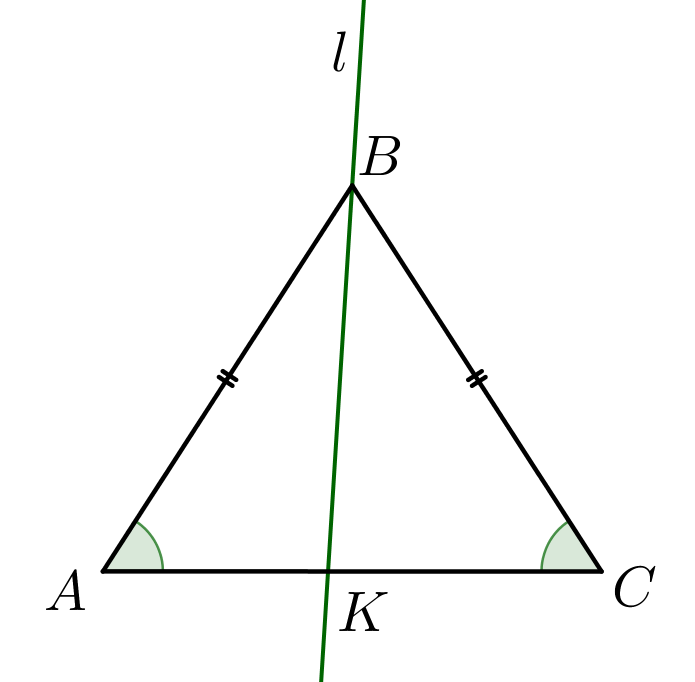
Теорема синусов
В треугольнике отношения сторон к синусам противолежащих углов одинаковы и равны удвоенному радиусу описанной окружности: \(\displaystyle \frac{\color{Purple}{a}}{\sin\color{Purple}{{\angle A}}}=\frac{\color{green}{b}}{\sin\color{green}{{\angle B}}}=\frac{\color{blue}{c}}{\sin\color{blue}{{\frac{\angle C}{2}}}}=2\color{red}{R}{\small.}\) | 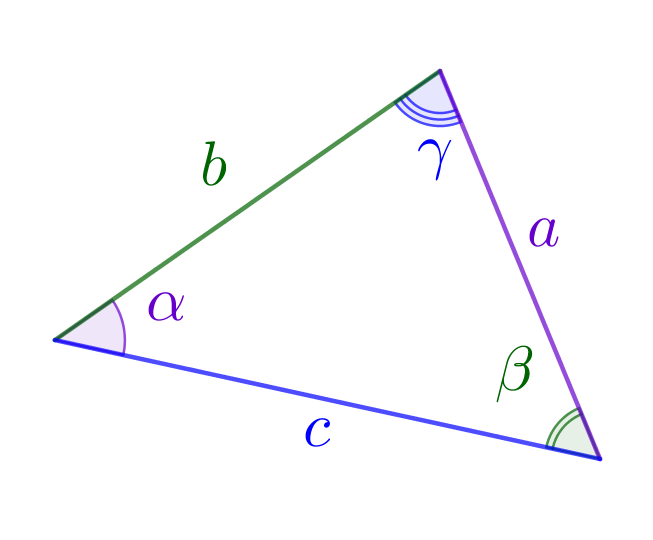 |
Треугольник \(\displaystyle ABC \)равнобедренный. Значит, угол \(\displaystyle BAC \)равен углу \(\displaystyle BCA{\small .} \) Выразим радиусы описанных окружностей через синусы этих углов, чтобы при нахождении отношения этих радиусов синусы сократились.
\(\displaystyle R_1=\frac{BK}{2\sin{\angle BAK}}\small.\)
Рассмотрим треугольник \(\displaystyle ABK\small.\) По теореме синусов: \(\displaystyle \frac{\color{green}{BK}}{\sin\color{green}{\angle BAK}}=2R_1\small.\) | 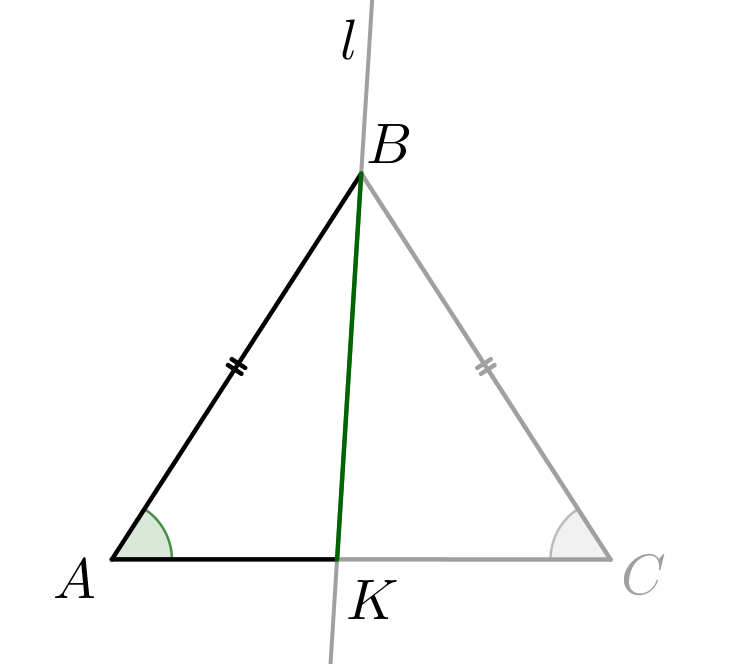 |
Выразим \(\displaystyle R_1\small{:}\)
\(\displaystyle R_1=\frac{BK}{2\sin{\angle BAK}}\small.\)
\(\displaystyle R_2=\frac{BK}{2\sin{\angle BCK}}\small.\)
Треугольник \(\displaystyle ABC\)- равнобедренный. Следовательно,
\(\displaystyle \angle BAK=\angle BCK\) и \(\displaystyle \sin \angle BAK=\sin \angle BCK\small.\)
Таким образом, радиусы окружностей, описанных около треугольников \(\displaystyle ABK\) и \(\displaystyle BCK\small,\) равны:
\(\displaystyle R_1=\frac{BK}{2\sin{\angle BAK}}=\frac{BK}{2\sin{\angle BCK}}=R_2\small.\)
Ответ: \(\displaystyle R_1:R_2=1\small.\)