Столб подпирает детскую горку посередине. Найдите высоту \(\displaystyle l\) этого столба, если высота \(\displaystyle h\) горки равна \(\displaystyle 3{,}2\)м. Ответ дайте в метрах.
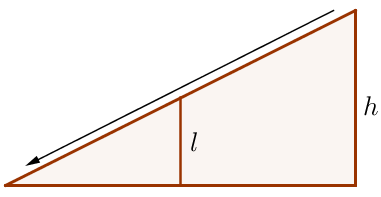
Изобразим предложенную в задаче конструкцию в виде прямоугольного треугольника \(\displaystyle ABC \small, \\ \) в котором \(\displaystyle \angle C =90^{\circ} \small, \) \(\displaystyle BC=3{,}2 \small. \)
По условию задачи столб длины \(\displaystyle l\) подпирает горку посередине.
Пусть точки \(\displaystyle N\) и \(\displaystyle M\) – середины сторон \(\displaystyle AB\) и \(\displaystyle AC\) соответственно.
Тогда \(\displaystyle NM\) – средняя линия треугольника \(\displaystyle ABC \) и \(\displaystyle NM=l \small. \) Средняя линия треугольника параллельна основанию и равна половине основания. Тогда \(\displaystyle NM= \frac{1}{2} \cdot BC \small, \) \(\displaystyle l= \frac{1}{2} \cdot 3{,}2=1{,}6 \small. \) | 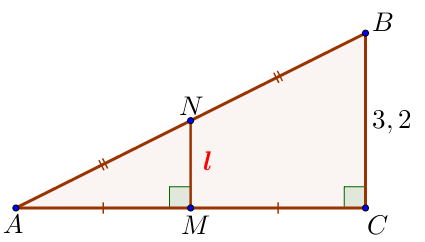 |
Ответ: \(\displaystyle 1{,}6 \small. \)