Задание
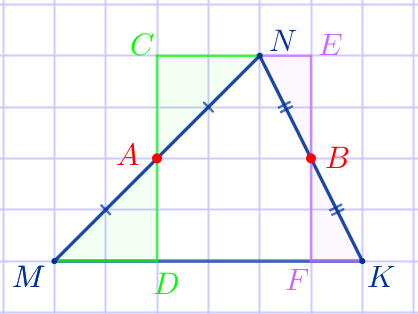
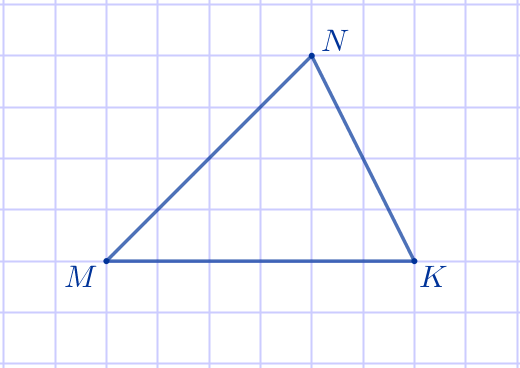
На клетчатой бумаге с размером клетки \(\displaystyle 1×1\) изображён треугольник \(\displaystyle MNK{\small.}\) Найдите длину его средней линии, параллельной стороне \(\displaystyle MK{\small.}\)
Решение
СПОСОБ \(\displaystyle 1{\small.}\) По определению.
Отметим на рисунке середины сторон треугольника \(\displaystyle MNK{\small:}\)
\(\displaystyle AB\) – средняя линия треугольника \(\displaystyle MNK{\small.}\) По рисунку определим длину \(\displaystyle AB{\small:}\) \(\displaystyle AB=3{\small.}\) |  |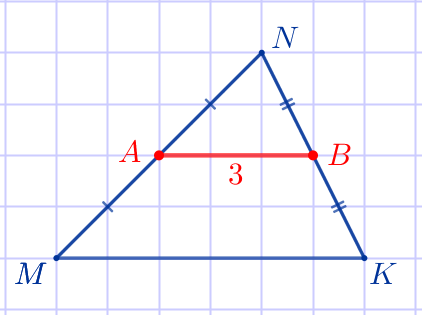
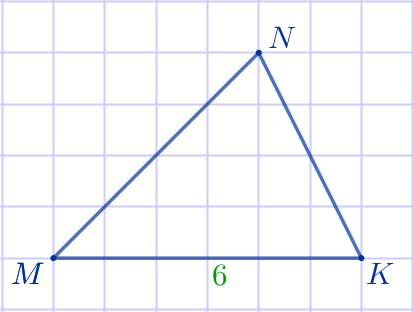СПОСОБ \(\displaystyle 2{\small.}\) По свойству средней линии треугольника.
 | По рисунку определим длину стороны \(\displaystyle MK{\small:}\) \(\displaystyle MK=6{\small.}\) Значит, длина средней линии треугольника, параллельной стороне \(\displaystyle MK{\small,}\) равна \(\displaystyle \frac{1}{2} \cdot MK=\frac{1}{2} \cdot 6=3{\small.}\) |
Ответ: \(\displaystyle 3{\small.}\)