Точки \(\displaystyle M\) и \(\displaystyle N\) являются серединами сторон \(\displaystyle AB\) и \(\displaystyle BC\) треугольника \(\displaystyle ABC\) соответственно. Отрезки \(\displaystyle AN\) и \(\displaystyle CM\) пересекаются в точке \(\displaystyle O{\small,}\) \(\displaystyle AN=15{\small,}\) \(\displaystyle CM=21{\small.}\) Найдите \(\displaystyle AO{\small.}\)
\(\displaystyle AO=\)
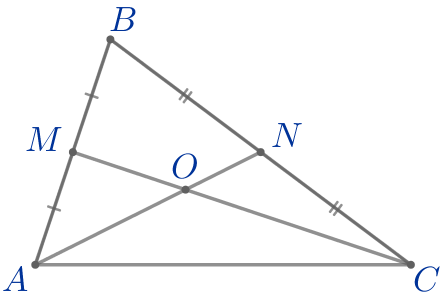 | \(\displaystyle ABC\) – треугольник:
Требуется найти \(\displaystyle AO{\small.}\) |
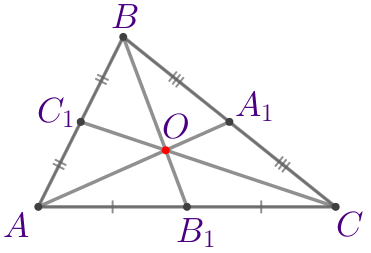
| Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении \(\displaystyle 2:1{\small,}\) считая от вершины. | |
| \(\displaystyle \frac{AO}{OA_1}=\frac{BO}{OB_1}=\frac{CO}{OC_1}=\frac{2}{1}\) |
По теореме о медианах треугольника
\(\displaystyle \frac{AO}{ON}=\frac{2}{1}{\small.}\)
Следовательно,
\(\displaystyle AO=\frac{2}{3} \cdot AN{\small.}\)
Подставим \(\displaystyle AN=15{\small.}\)
\(\displaystyle AO=\frac{2}{3}\cdot 15=10{\small.}\)
Ответ: \(\displaystyle AO=10{\small.}\)