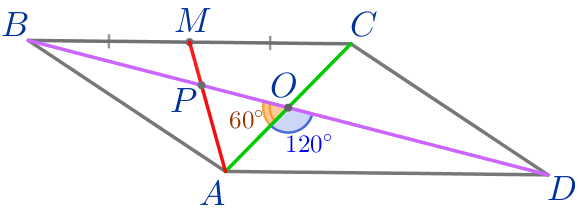
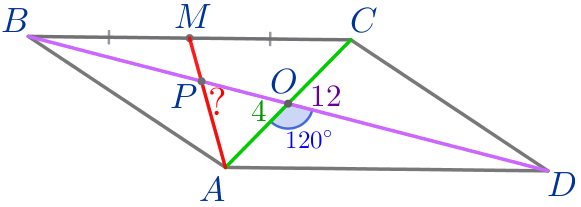
В параллелограмме \(\displaystyle ABCD\) диагонали пересекаются в точке \(\displaystyle O{\small,}\) точка \(\displaystyle M\) – середина стороны \(\displaystyle BC{\small.}\) Найдите \(\displaystyle AM{\small,}\) если \(\displaystyle BD=12{\small,}\) \(\displaystyle AC=4{\small,}\) а угол \(\displaystyle AOD\) равен \(\displaystyle 120^{\circ}{\small.}\)
\(\displaystyle AM=\)
\(\displaystyle ABCD\) – параллелограмм:
 |
|
Требуется найти длину отрезка \(\displaystyle AM{\small.}\)
\(\displaystyle \angle AOP=60^{\circ}{\small.}\)
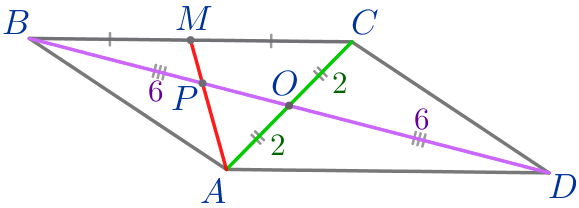
\(\displaystyle AO=OC=2{\small;}\)
\(\displaystyle BO=OD=6{\small;}\)
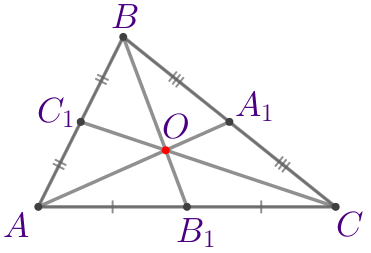
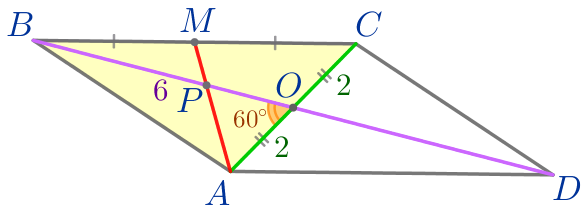 | Точки \(\displaystyle M\) и \(\displaystyle O\) – середины сторон \(\displaystyle BC\) и \(\displaystyle AC\) соответственно, следовательно, \(\displaystyle AM\) и \(\displaystyle BO\) – медианы треугольника \(\displaystyle ABC{\small.}\) |
\(\displaystyle \frac{BP}{PO}=\frac{AP}{PM}=\frac{2}{1}{\small.}\)
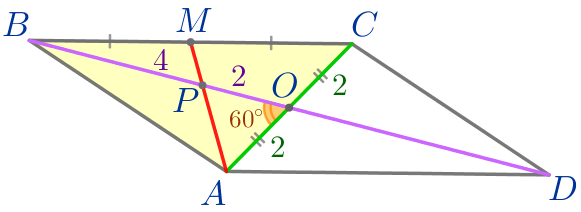 | Следовательно:
|
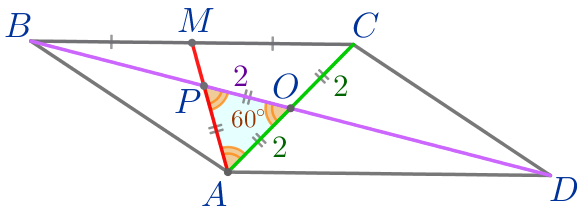 | \(\displaystyle \color{blue}{1)}\) \(\displaystyle OA=OP=2{\small,}\) значит, \(\displaystyle \triangle AOP\) – равнобедренный. \(\displaystyle \color{blue}{2)}\) В равнобедренном треугольнике углы при основании равны, значит, |
\(\displaystyle \angle OAP= \angle OPA=\frac{180^{\circ}-\angle AOP}{2}=\frac{180^{\circ}-60^{\circ}}{2}=\frac{120^{\circ}}{2}=60^{\circ}{\small.}\)
\(\displaystyle \color{blue}{3)}\) Все углы треугольника \(\displaystyle AOP\) равны \(\displaystyle 60^{\circ}{\small,}\) значит,
\(\displaystyle \triangle AOP\) – равносторонний.
В равностороннем треугольнике все стороны равны, то есть
\(\displaystyle AP=OA=OP=2{\small.}\)
 |
|
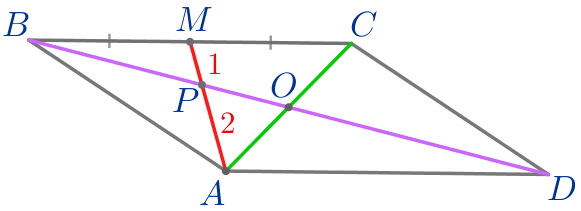
Значит,
\(\displaystyle PM=\frac{1}{2} \cdot AP=\frac{1}{2} \cdot 2=1{\small.}\)
Так как точка \(\displaystyle P\) лежит на отрезке \(\displaystyle AM{\small,}\) то
\(\displaystyle AM=AP+PM=2+1=3{\small.}\)
Ответ: \(\displaystyle AM=3{\small.}\)