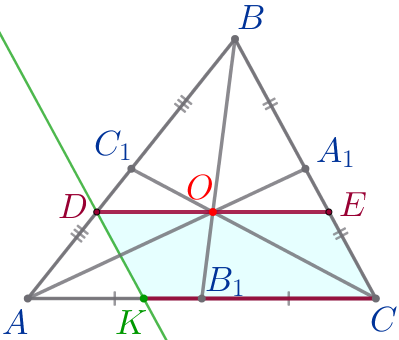
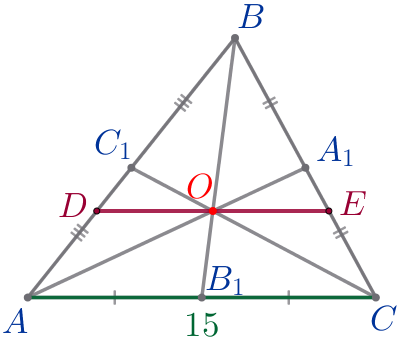
Через точку пересечения медиан треугольника \(\displaystyle ABC\) проведен отрезок \(\displaystyle DE{\small,}\) параллельный стороне \(\displaystyle AC{\small.}\) Точки \(\displaystyle D\) и \(\displaystyle E\) лежат на сторонах \(\displaystyle AB\) и \(\displaystyle BC\) соответственно. Найдите длину \(\displaystyle DE{\small,}\) если \(\displaystyle AC=15{\small.}\)
\(\displaystyle DE=\)
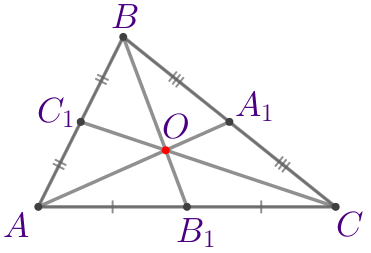
 | \(\displaystyle ABC\) – треугольник:
Требуется найти длину отрезка \(\displaystyle DE{\small.}\) |
Выполним дополнительное построение.
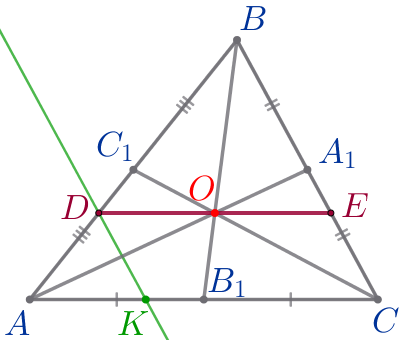 | Через точку \(\displaystyle D\) параллельно стороне \(\displaystyle BC\) проведём прямую \(\displaystyle DK{\small.}\) \(\displaystyle K\) – точка пересечения \(\displaystyle DK\) и \(\displaystyle AC{\small.}\) |
\(\displaystyle DE=KC{\small.}\)
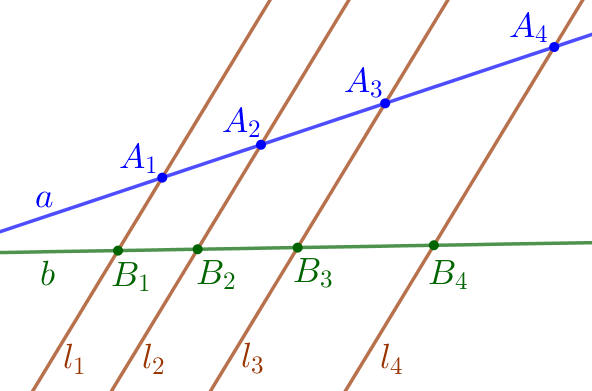
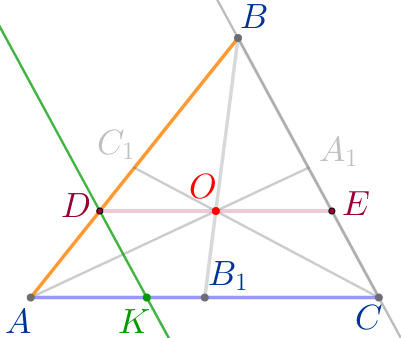 | Согласно теореме о пропорциональных отрезках: \(\displaystyle \frac{KC}{BD}=\frac{AK}{DA}{\small.}\) По свойству пропорции получаем: \(\displaystyle \color{blue}{\frac{KC}{AK}=\frac{BD}{DA}}{\small.}\) |
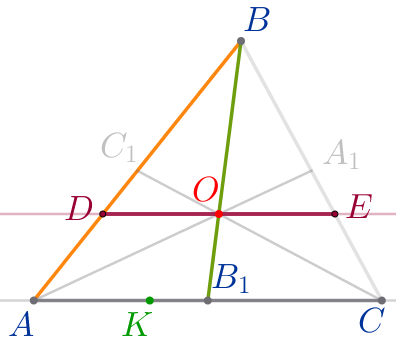 | Согласно теореме о пропорциональных отрезках: \(\displaystyle \frac{BD}{BO}=\frac{DA}{OB_1}{\small.}\) По свойству пропорции получаем: \(\displaystyle \color{blue}{\frac{BD}{DA}=\frac{BO}{OB_1}}{\small.}\) |
\(\displaystyle \color{blue}{\frac{BO}{OB_1}=\frac{2}{1}}{\small.}\)
В результате получаем:
\(\displaystyle \color{blue}{\frac{KC}{AK}=\frac{BD}{DA}=\frac{BO}{OB_1}=\frac{2}{1}}{\small.}\)
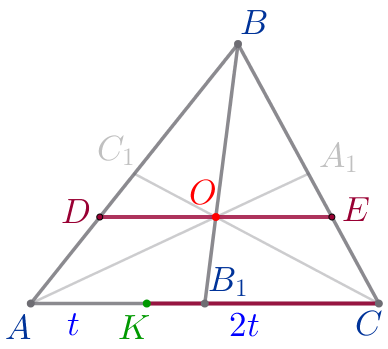 | То есть \(\displaystyle KC=2t{\small,}\) \(\displaystyle AK=t{\small.}\) Так как точка \(\displaystyle K\) лежит на отрезке \(\displaystyle AC{\small,}\) то \(\displaystyle AC=AK+KC=t+2t=3t{\small.}\) Тогда \(\displaystyle \frac{KC}{AC}=\frac{2t}{3t}=\frac{2}{3}{\small.}\) |
Следовательно,
\(\displaystyle KC=\frac{2}{3}\cdot AC{\small.}\)
Подставим \(\displaystyle AC=15{\small:}\)
\(\displaystyle KC=\frac{2}{3}\cdot 15=10{\small.}\)
Поскольку \(\displaystyle DE=KC{\small,}\) значит, \(\displaystyle DE=10{\small.}\)
Ответ: \(\displaystyle DE=10{\small.}\)