Даны два треугольника \(\displaystyle ABC\) и \(\displaystyle A_1B_1C_1\) такие, что \(\displaystyle AC=14\, {\footnotesize см} {\small,}\) \(\displaystyle A_1B_1=22\, {\footnotesize см} {\small,}\) \(\displaystyle B_1C_1=26\, {\footnotesize см} {\small,}\) \(\displaystyle A_1C_1=28\, {\footnotesize см} {\small,}\) \(\displaystyle AB=11\, {\footnotesize см} {\small,}\) \(\displaystyle BC=13\, {\footnotesize см} {\small.}\)
\(\displaystyle \color{red}{1{\small.}}\) Верно ли, что \(\displaystyle \triangle ABC \sim \triangle A_1B_1C_1{\small?}\)
\(\displaystyle \color{red}{2 {\small.}}\) Почему?
Выполним построение по условию задачи и рассмотрим треугольники \(\displaystyle ABC\) и \(\displaystyle A_1B_1C_1{\small:}\)
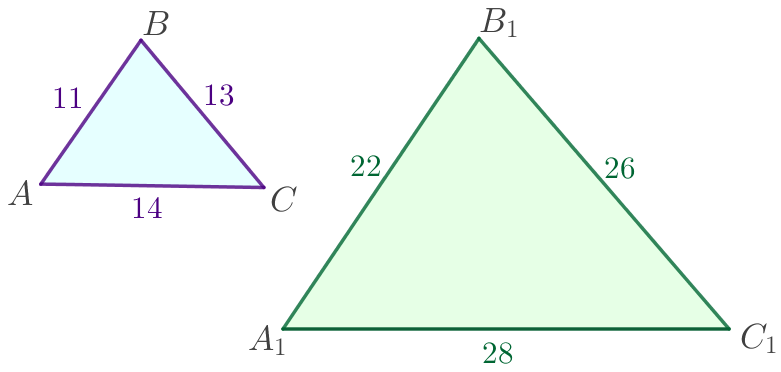
\(\displaystyle \frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}=\frac{1}{2}{\small.}\)
Значит,
\(\displaystyle \triangle ABC \sim \triangle A_1B_1C_1\) по трём сторонам (по третьему признаку подобия)
| Ответ: | \(\displaystyle \color{red}{1{\small.}}\) Да. |
| \(\displaystyle \color{red}{2{\small.}}\) По третьему признаку подобия (по трём сторонам). |