В треугольнике \(\displaystyle ABC\) \(\displaystyle AB=4{\small,}\) \(\displaystyle BC=6{\small,}\) \(\displaystyle AC=9{\small.}\) Точка \(\displaystyle E\) лежит на стороне \(\displaystyle BC{\small.}\) Внутри треугольника взята точка \(\displaystyle M\) так, что \(\displaystyle MB=1{\small \frac{7}{9}}{\small,}\) \(\displaystyle ME=2 {\small \frac{2}{3}}{\small,}\) \(\displaystyle CE=2{\small.}\) Укажите угол, равный углу \(\displaystyle BEM{\small.}\)
\(\displaystyle \angle BEM=\)
По условию задачи выполним построение и рассмотрим треугольники \(\displaystyle ABC\) и \(\displaystyle BME{\small.}\)
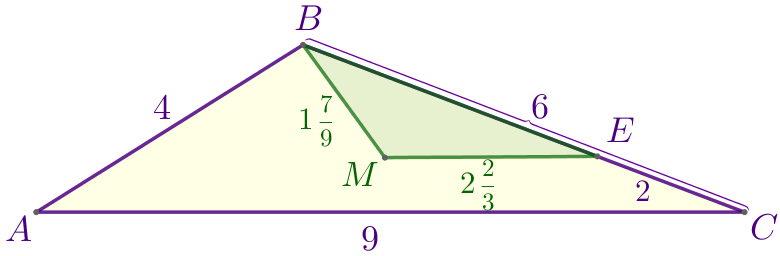
В треугольнике \(\displaystyle ABC{\small:}\)
| В треугольнике \(\displaystyle BME{\small:}\)
|
Найдём отношения меньших , средних и бóльших сторон треугольников.
| \(\displaystyle \triangle ABC\) | \(\displaystyle \triangle BME\) | отношение сторон | |
| меньшая сторона | \(\displaystyle 4\) | \(\displaystyle 1\frac{7}{9}=\frac{16}{9}\) | \(\displaystyle 4:\frac{16}{9}=\frac{4\cdot 9}{16}=\color{red}{\frac{9}{4}}\) |
| средняя сторона | \(\displaystyle 6\) | \(\displaystyle 2\frac{2}{3}=\frac{8}{3}\) | \(\displaystyle 6:\frac{8}{3}=\frac{6\cdot 3}{8}=\color{red}{\frac{9}{4}}\) |
| бóльшая сторона | \(\displaystyle 9\) | \(\displaystyle 4\) | \(\displaystyle \color{red}{\frac{9}{4}}\) |
Отношения сходственных сторон равны, значит, треугольник \(\displaystyle ABC\) подобен треугольнику \(\displaystyle BME{\small.}\)
В подобных треугольниках напротив сходственных сторон лежат соответственно равные углы.
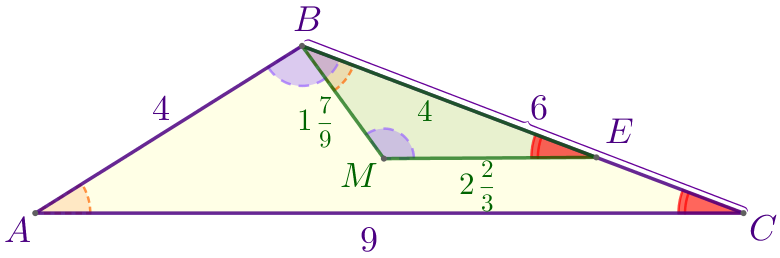
Следовательно,
\(\displaystyle \angle BEM=\angle ACB{\small.}\)
Ответ: \(\displaystyle \angle BEM=\angle ACB{\small.}\)