В треугольнике \(\displaystyle ABC\) \(\displaystyle AB=9{\small,}\) \(\displaystyle BC=12{\small,}\) \(\displaystyle AC=18{\small.}\) В треугольнике \(\displaystyle DEF\) \(\displaystyle DE=3{\small,}\) \(\displaystyle EF=4{\small,}\) \(\displaystyle DF=6{\small.}\) Укажите верное утверждение.
Выполним построение по условию задачи и рассмотрим треугольники \(\displaystyle ABC\) и \(\displaystyle DEF{\small:}\)
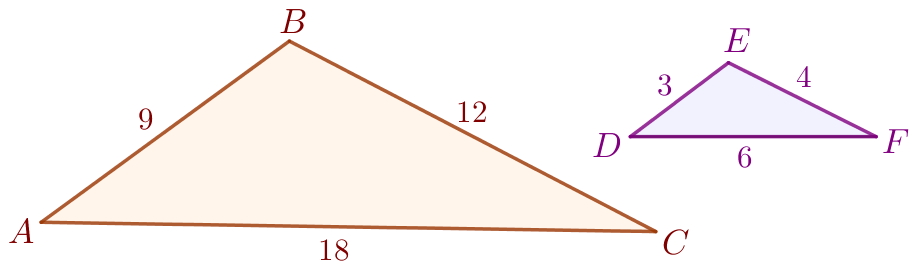
\(\displaystyle \frac{AB}{DE}=\frac{BC}{EF}=\frac{AC}{DF}=3{\small.}\)
Значит,
\(\displaystyle \triangle ABC \sim \triangle DEF\) по трём сторонам (по третьему признаку подобия)
В подобных треугольниках напротив сходственных сторон лежат соответственно равные углы. Следовательно,
\(\displaystyle \angle A=\angle D{\small,}\) \(\displaystyle \angle B=\angle E{\small,}\) \(\displaystyle \angle C=\angle F{\small.}\)
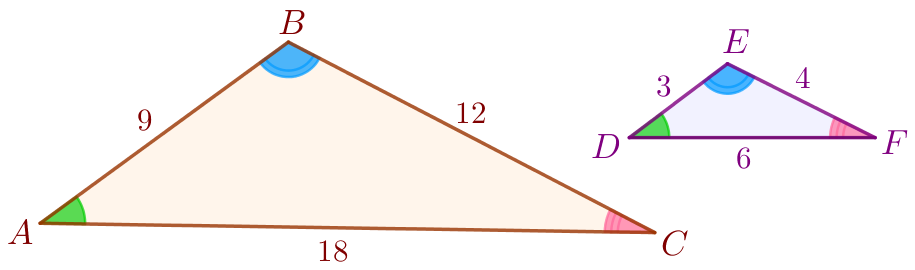
Ответ: \(\displaystyle \angle A=\angle D{\small,}\) \(\displaystyle \angle B=\angle E{\small,}\) \(\displaystyle \angle C=\angle F{\small.}\)