Теория: 17 Решение треугольников с применением тригонометрических соотношений (короткая версия)

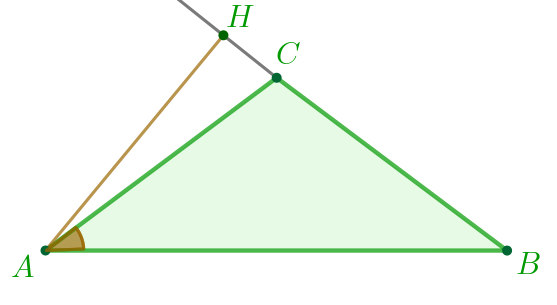
По условию: \(\displaystyle AC=BC{\small , }\) \(\displaystyle AB=15{\small,}\) \(\displaystyle AH\) – высота и \(\displaystyle \cos\angle BAC=0{,}6{\small . }\)

Пусть \(\displaystyle \angle BAC=\alpha{\small.}\) Треугольник  \(\displaystyle ABC\) равнобедренный. Следовательно, \(\displaystyle \angle BAC=\angle ABC=\alpha{\small.}\)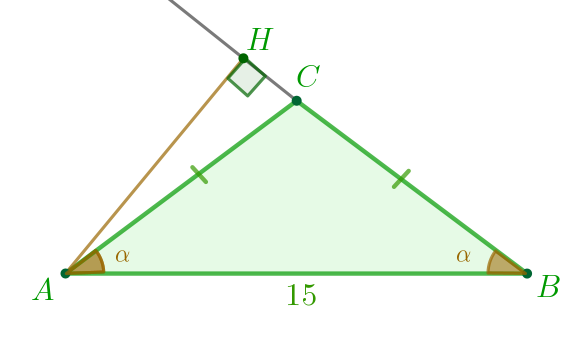

Высоту \(\displaystyle AH\) найдем из прямоугольного треугольника \(\displaystyle ABH{\small.}\)

СПОСОБ \(\displaystyle 1\)

По условию \(\displaystyle AB=15{\small,}\)\(\displaystyle \cos\alpha=0{,}6{\small .}\)

По определению косинуса в прямоугольном треугольнике

\(\displaystyle \cos\alpha=\frac{BH}{AB}{\small .}\) Значит, \(\displaystyle BH=AB \cdot \cos \alpha{\small;}\) \(\displaystyle BH=15 \cdot 0{,}6=9{\small.}\)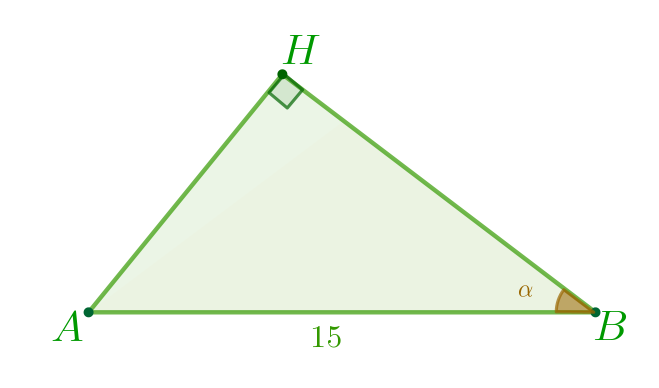

С помощью теоремы Пифагора найдем катет  \(\displaystyle AH{\small:}\)

\(\displaystyle AB^2=AH^2+BH^2{\small;}\)

\(\displaystyle AH^2=AB^2-BH^2{\small;}\)

\(\displaystyle AH^2=15^2-9^2=225-81=144{\small.}\)

Так как длина отрезка положительна, то \(\displaystyle AH=12{\small.}\)

СПОСОБ \(\displaystyle 2\)

По определению синуса угла в прямоугольном треугольнике

\(\displaystyle \frac{AH}{AB}=\sin \alpha{\small.}\) Значит, \(\displaystyle AH=AB \cdot \sin \alpha{\small;}\) \(\displaystyle AH=15 \cdot \sin \alpha{\small.}\)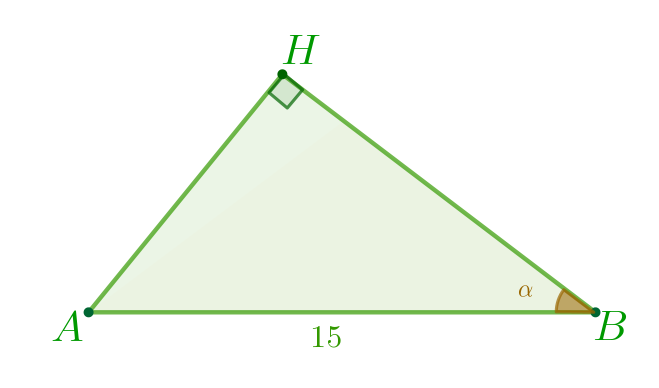

Для вычисления сунуса угла воспользуемся основным тригонометрическим тождеством:

\(\displaystyle \sin^2 \alpha+\cos^2 \alpha=1{\small;}\)

\(\displaystyle \sin^2\alpha = 1 - \cos^2\alpha{\small.}\)

Подставим \(\displaystyle \cos\alpha=0{,}6{\small :}\)

\(\displaystyle \sin^2\alpha=1-0{,}6^2{\small;}\)

\(\displaystyle \sin^2\alpha=1-0{,}36{\small;}\)

\(\displaystyle \sin^2\alpha=0{,}64{\small;}\)

\(\displaystyle \sin\alpha=0{,}8{\small .}\)

В результате получаем

\(\displaystyle AH=15 \cdot \sin \alpha=15\cdot 0{,}8=12 {\small.}\)

Ответ:  \(\displaystyle 12{\small .}\)