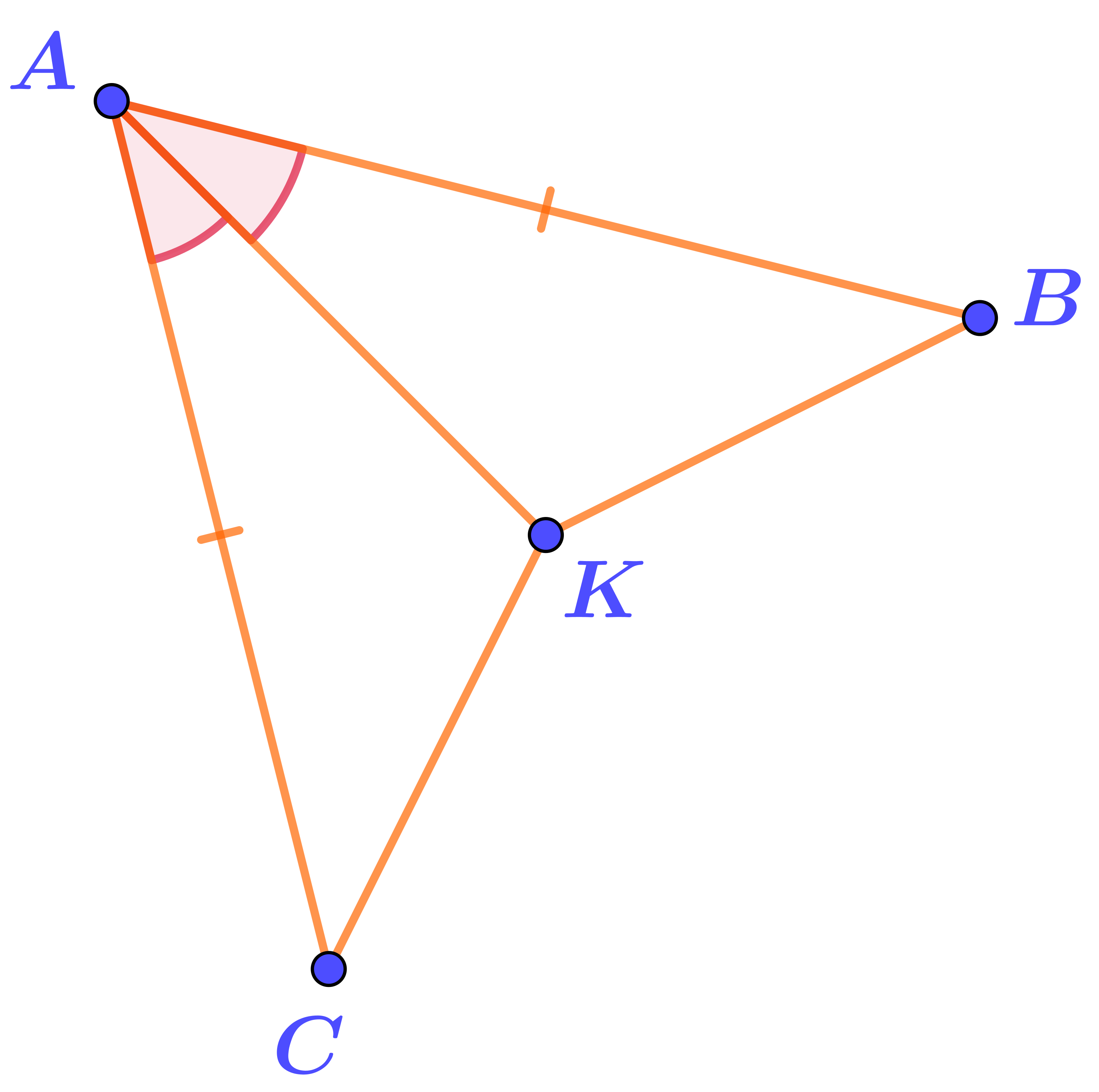
Два треугольника имеют общую сторону \(\displaystyle AK{\small .}\)
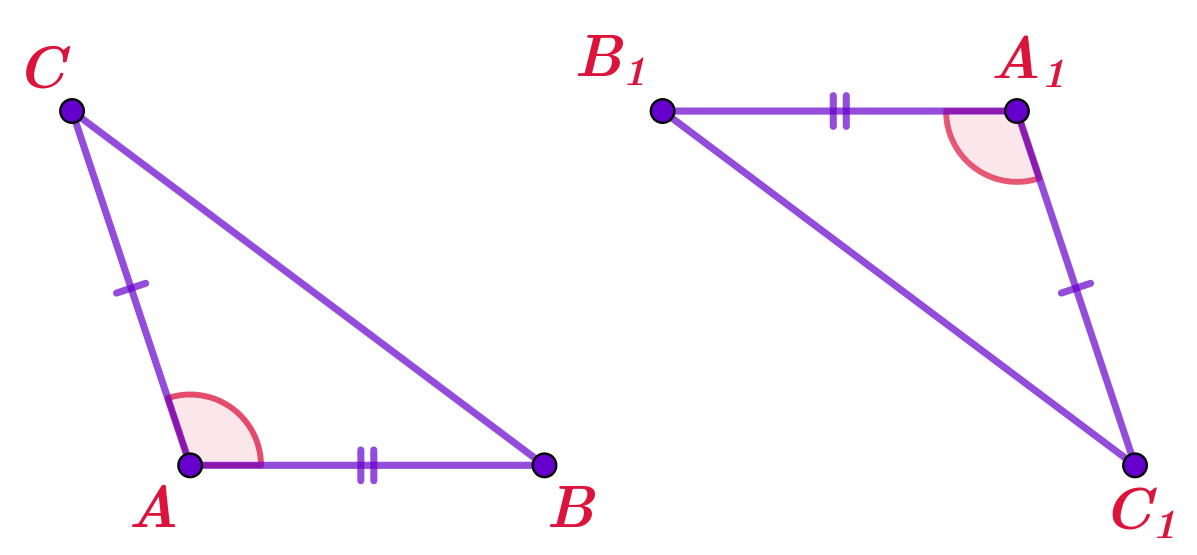
На рисунке обозначены равные углы и отрезки.
Известно, что \(\displaystyle \angle ABK=44\degree{\small .}\)
Найдите величину угла \(\displaystyle KCA{\small .}\) Ответ дайте в градусах.
\(\displaystyle \angle KCA=\)\(\displaystyle \degree \)
1. Рассмотрим треугольники \(\displaystyle AKB\) и \(\displaystyle AKC\)
Запись доказательства:
\(\displaystyle \left\{\begin{array}{ll}AB=AC\\AK - { \normalsize\itобщая}\,{\normalsize\itсторона}\\\angle KAB =\angle KAC\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}AKB={\bf\triangle}AKC\text{ \normalsize\it(по первому признаку)}\right.\)
2. Значит, равны и углы, расположенные в равных треугольниках напротив общей стороны:
\(\displaystyle \angle KCA=\angle KBA=\)\(\displaystyle \bf 44\degree{\small .}\)
Ответ: \(\displaystyle 44\degree{\small .}\)