Вершина \(\displaystyle C\) треугольника \(\displaystyle ABC\) соединена с серединой \(\displaystyle D\) противоположной стороны \(\displaystyle AB\) .
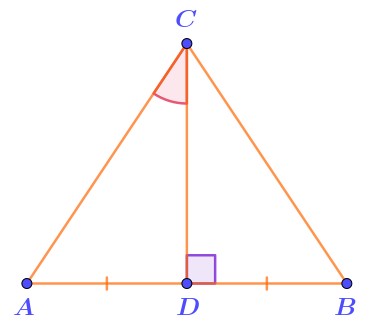
Известно, что \(\displaystyle \angle ACD=37\degree \) и \(\displaystyle \angle BDC=90\degree {\small .}\)
Найдите величину угла \(\displaystyle ACB{\small .}\) Ответ дайте в градусах.
\(\displaystyle \angle ACB=\)\(\displaystyle \degree \)
Величина угла \(\displaystyle ACB\) равна сумме величин его частей:
\(\displaystyle \angle ACB=\angle ACD+\angle BCD{\small .}\)
Чтобы узнать величину угла \(\displaystyle BCD{\small ,}\) нужно найти равный ему угол известной величины.
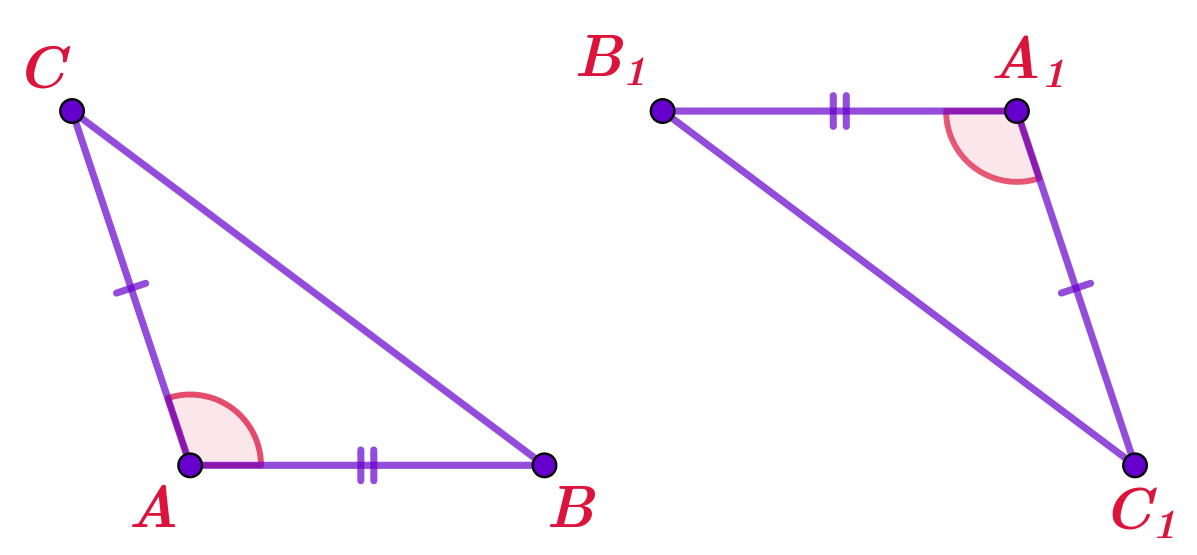
Равные углы можно найти в равных треугольниках. Докажем, что равны треугольники \(\displaystyle ACD\) и \(\displaystyle BCD{\small .}\)
Отметим равные и общие элементы на рисунке.
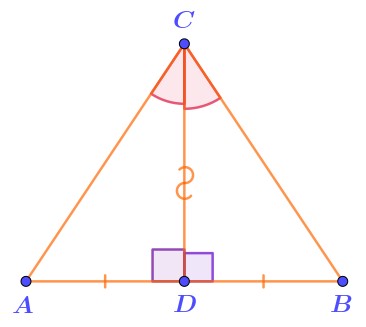
Для треугольников \(\displaystyle ACD\) и \(\displaystyle BCD\) выполняются условия первого признака равенства треугольников:
\(\displaystyle \left\{\begin{array}{ll}AD=BD\\CD -\text{ \normalsize\itобщая\, сторона}\\\angle ADC=\angle BDC \end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}ACD={\bf\triangle}BCD\text{ \normalsize\it(по первому признаку)}\right.\)
3. Из равенства треугольников следует равенство углов, лежащих напротив равных сторон \(\displaystyle BD\) и \(\displaystyle AD\):
\(\displaystyle \angle BCD=\angle ACD=37\degree {\small .}\)
4. Приходим к ответу на вопрос задачи:
\(\displaystyle \angle ACB=\angle ACD+\angle BCD=37\degree +37\degree =\)\(\displaystyle \bf 74\degree {\small .}\)
Ответ: \(\displaystyle 74\degree{\small .}\)