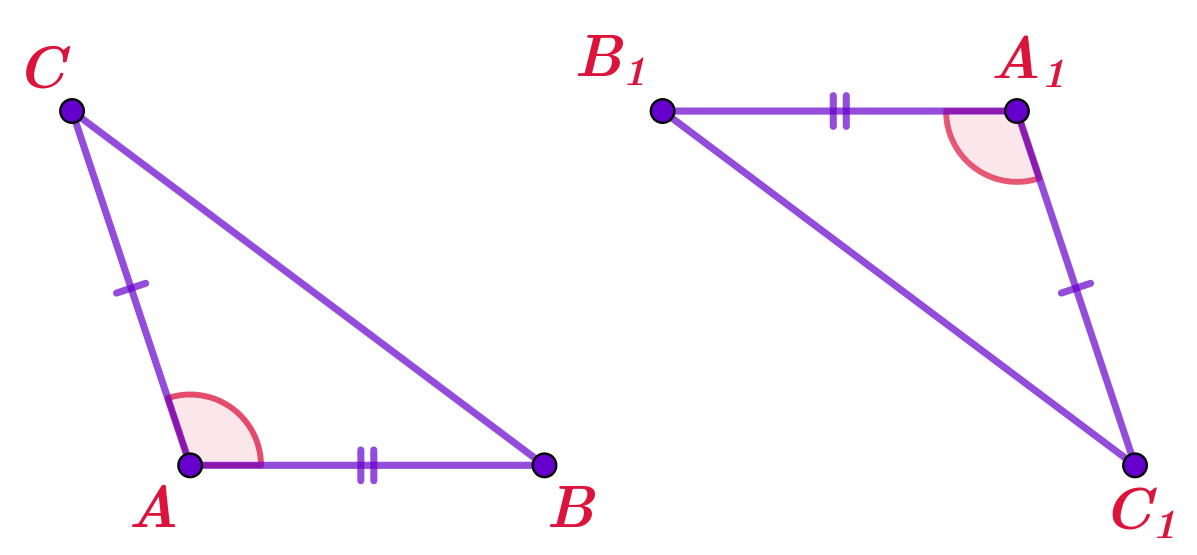
На рисунке изображён четырёхугольник \(\displaystyle PDQB{\small .}\)
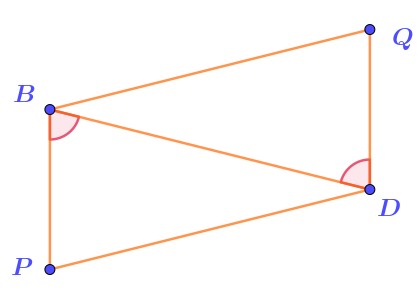
Известны длины трёх его сторон: \(\displaystyle BP=7{\small ,}\)\(\displaystyle PD=10{\small ,}\)\(\displaystyle DQ=7{\small .}\)
Кроме того, известно, что \(\displaystyle \angle PBD=\angle BDQ{\small .}\)
Найти периметр четырёхугольника \(\displaystyle PDQB{\small .}\)
\(\displaystyle P=\)
Периметр четырёхугольника \(\displaystyle BPDQ\) \(\displaystyle -\) сумма длин всех четырёх сторон.
Чтобы найти неизвестную сторону \(\displaystyle BQ\), найдём равный ей отрезок с известной длиной.
Для этого найдём равные треугольники, где пара этих отрезков \(\displaystyle -\) равные стороны.
1. Заметим, что две стороны четырёхугольника равны, так как равны их длины:
\(\displaystyle PB=7=QD{\small .}\)
Отметим на рисунке эти равные стороны и общую сторону треугольников \(\displaystyle PBD\) и \(\displaystyle QDB{\small .}\)
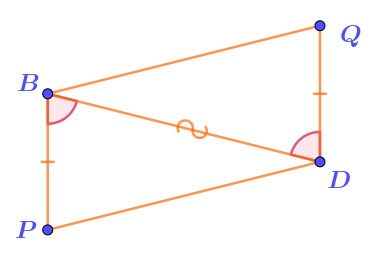
2. Рассмотрим треугольники \(\displaystyle PBD\) и \(\displaystyle QDB{\small .}\)
Запись доказательства:
\(\displaystyle \left\{\begin{array}{ll}PB=DQ\\BD -\text{ \normalsize\itобщая\, сторона}\\\angle PBD=\angle QDB\end{array} {\LARGE\Rightarrow} \quad {\bf\triangle}PBD={\bf\triangle}QBD\text{ \normalsize\it(по первому признаку)}\right.\)
3. В равных треугольниках равны стороны, расположенные напротив равных углов:
\(\displaystyle QB=PD=10{\small .}\)
4. Вычислим периметр как сумму длин сторон:
\(\displaystyle P_{BPDQ}=BP+PD+DQ+QB=7+10+7+10=\)\(\displaystyle \bf 34{\small .}\)
Ответ: \(\displaystyle 34{\small .}\)