Задание
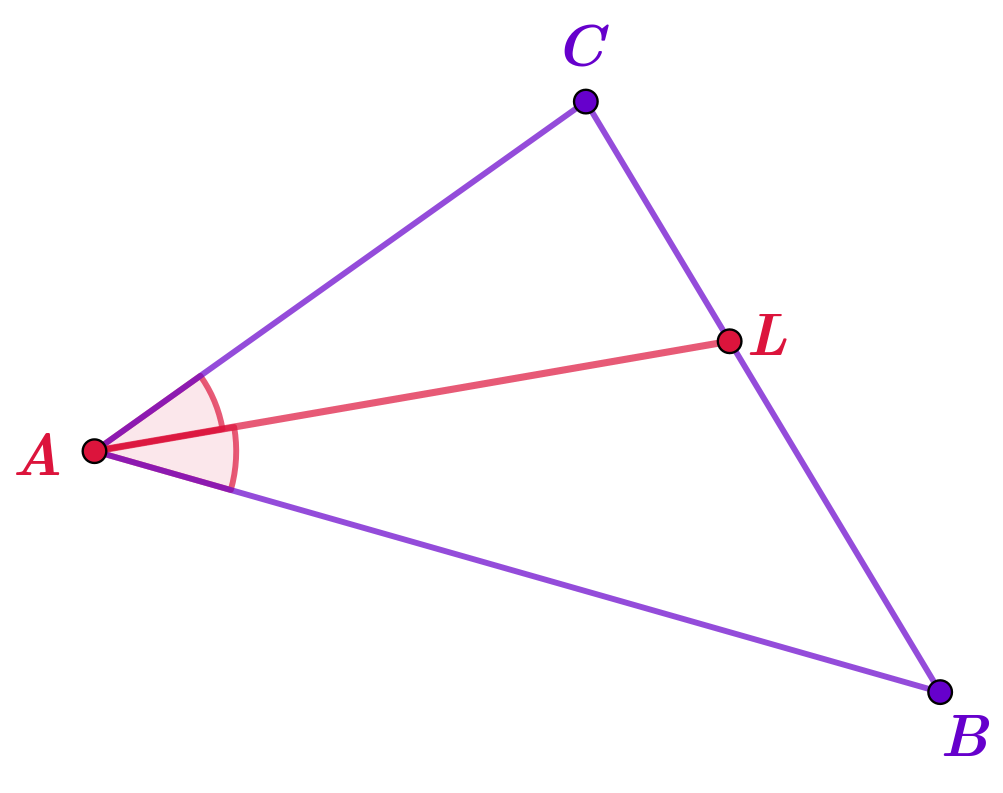
В треугольнике \(\displaystyle ABC\) проведена биссектриса \(\displaystyle AL{\small .}\)
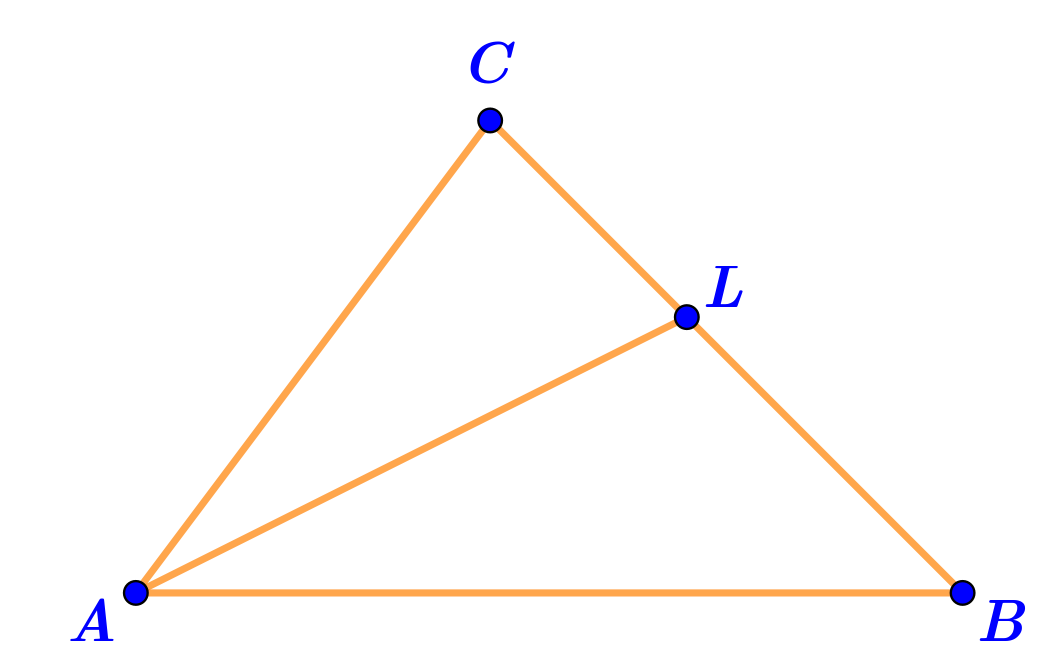
Величина угла \(\displaystyle BAL\) равна \(\displaystyle 31\degree {\small .}\)
Сколько градусов составляет величина угла \(\displaystyle BAC\,?\)
\(\displaystyle \angle BAC=\)\(\displaystyle \degree \)
Решение
Пользуясь определением биссектрисы, отметим на рисунке равные углы
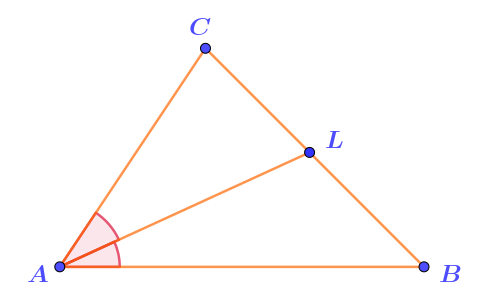
Найдём величину угла \(\displaystyle BAC\) как сумму величин двух его равных частей:
\(\displaystyle \angle BAC=\angle BAL+\angle CAL=31\degree +31\degree =\)\(\displaystyle 62\degree {\small .}\)
Ответ: \(\displaystyle 62\degree {\small .}\)