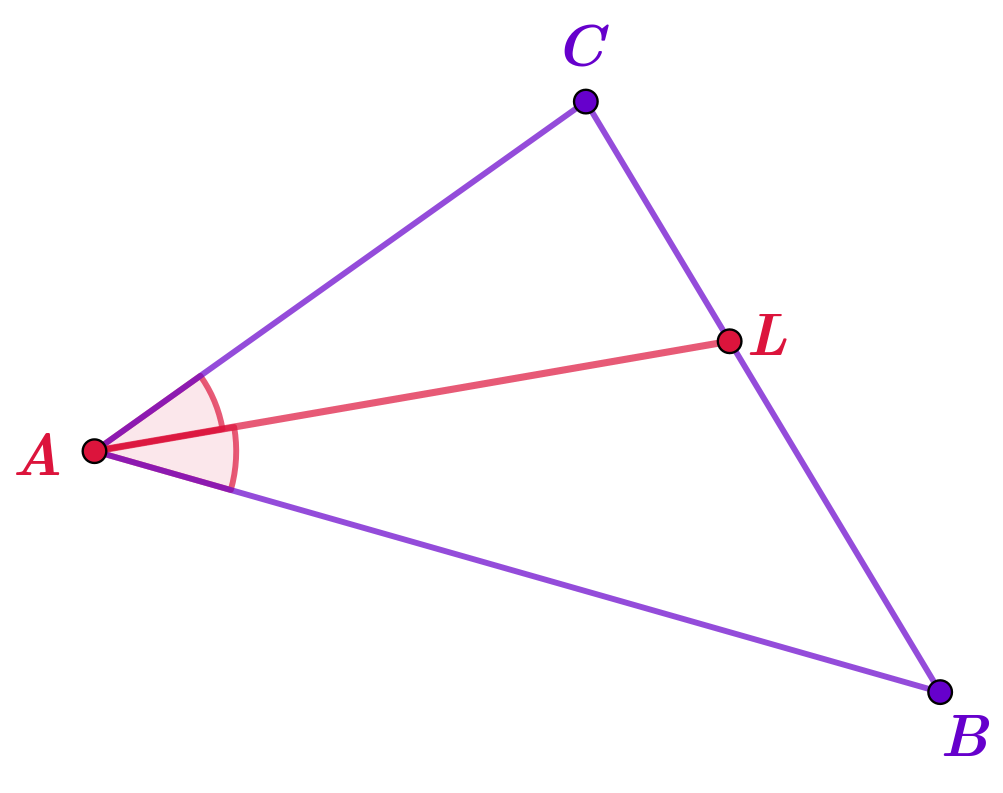
В треугольнике \(\displaystyle ABC\) провели несколько отрезков, соединяющих вершину \(\displaystyle C\) с точками на стороне \(\displaystyle AB{\small .}\)
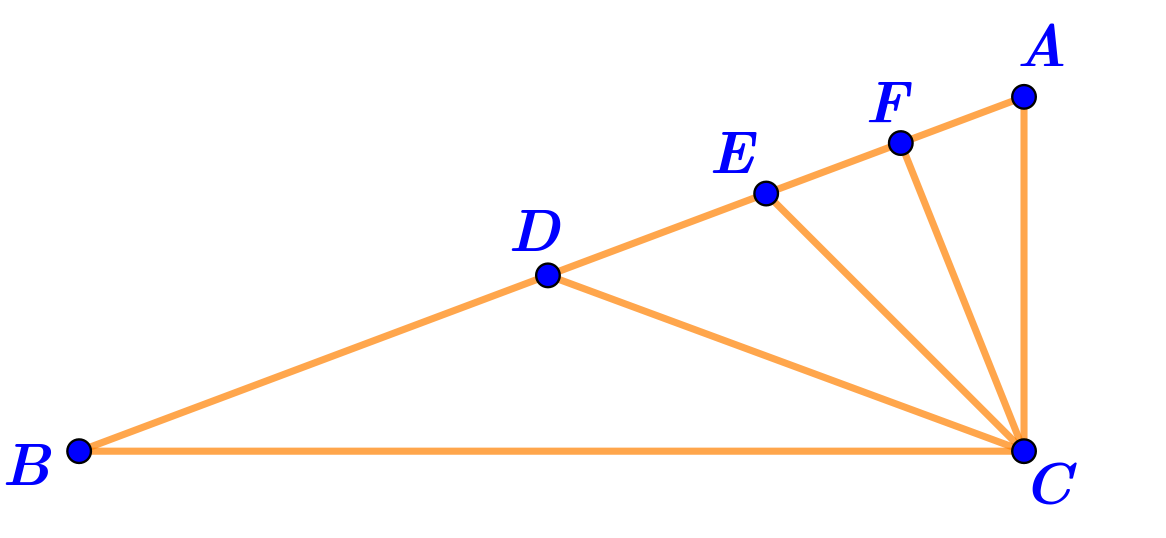
Известно, что \(\displaystyle \angle ACB=\angle AFC=90\degree {\small ,\;}AD=BD{\small ,\;}\angle ACE=\angle BCE{\small .}\)
Какой из отрезков, изображённых на рисунке, является биссектрисой треугольника \(\displaystyle ABC{\small ?}\)
В условиях задачи есть две пары равных углов:
\(\displaystyle \angle ACB=\angle AFC=90\degree\;\;\) и \(\displaystyle \;\;\angle ACE=\angle BCE{\small .}\)
Отметим их на рисунке.
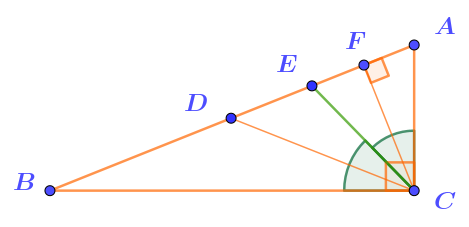
Отрезок \(\displaystyle CE\) разделил угол при вершине \(\displaystyle C\) на две равные части. По определению, это и есть биссектриса.
Ответ: биссектрисой треугольника \(\displaystyle ABC\) является отрезок \(\displaystyle CE{\small .}\)