Окружность, вписанная в треугольник \(\displaystyle ABC\small,\) касается стороны \(\displaystyle AB\) в точке \(\displaystyle K\small,\) при этом \(\displaystyle AK=1\small,\) \(\displaystyle BK=4\small.\) Найдите \(\displaystyle CK\small,\) если \(\displaystyle \angle BAC=120^{\circ}\small.\)
Отрезки касательных равны. Значит,
| 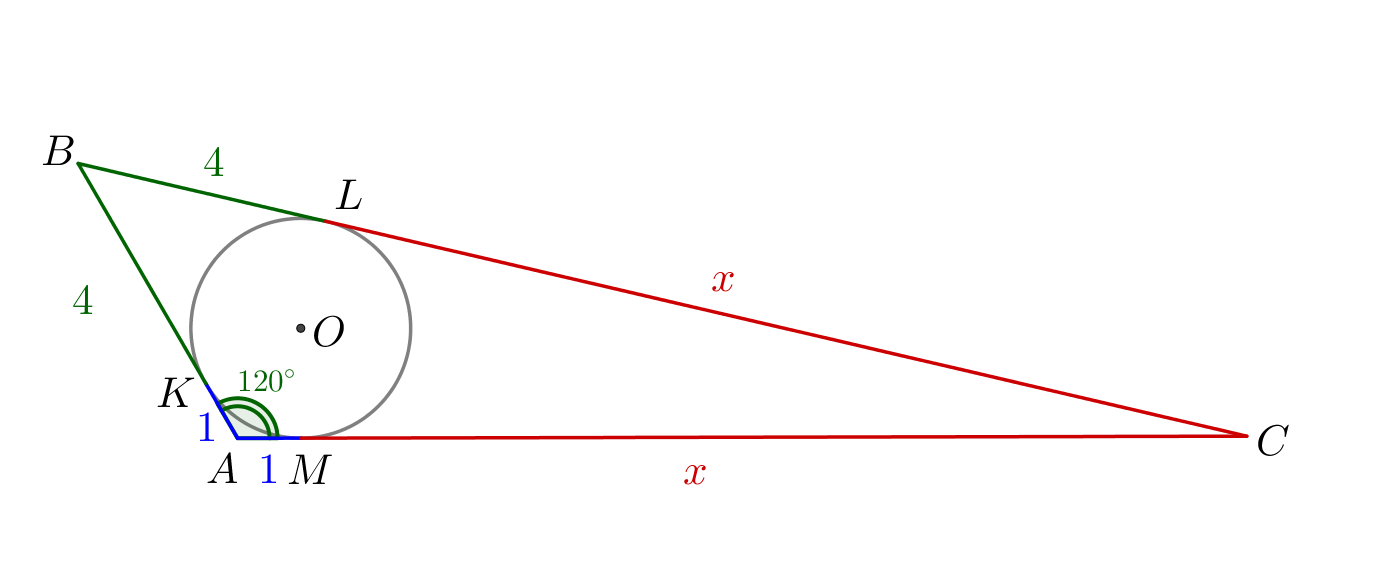 |
Тогда чтобы решить задачу,
- найдем \(\displaystyle x\small,\) используя теорему косинусов для треугольника \(\displaystyle ABC\small;\)
- зная \(\displaystyle AC\) и \(\displaystyle AK\small,\) найдем \(\displaystyle CK\) по теореме косинусов для треугольника \(\displaystyle AKC\small.\)
\(\displaystyle x=15\small.\)
Запишем теорему косинусов для стороны \(\displaystyle BC{\small:}\)
\(\displaystyle (4+x)^2=(1+4)^2+(1+x)^2-2(1+4)(1+x)\cos120^{\circ}\small.\)
Упростим выражение:
\(\displaystyle (4+x)^2=5^2+(1+x)^2-2\cdot5\cdot(1+x) \Big(-\frac{1}{2}\Big)\small,\)
\(\displaystyle \color{blue}{(4+x)^2}=25+\color{green}{(1+x)^2}+\color{purple}{5\cdot(1+x)}\small.\)
Раскроем скобки и упростим выражение:
\(\displaystyle \color{blue}{16+8x+x^2}=25+\color{green}{1+2x+x^2}+\color{purple}{5+5x}\small,\)
\(\displaystyle 16+8x+\cancel{x^2}=31+7x+\cancel{x^2}\small.\)
Перенесем все слагаемые с \(\displaystyle x\) влево, а числа вправо:
\(\displaystyle 8x-7x=31-16\small,\)
\(\displaystyle x=15\small.\)
\(\displaystyle CK=\sqrt{273}\small.\)
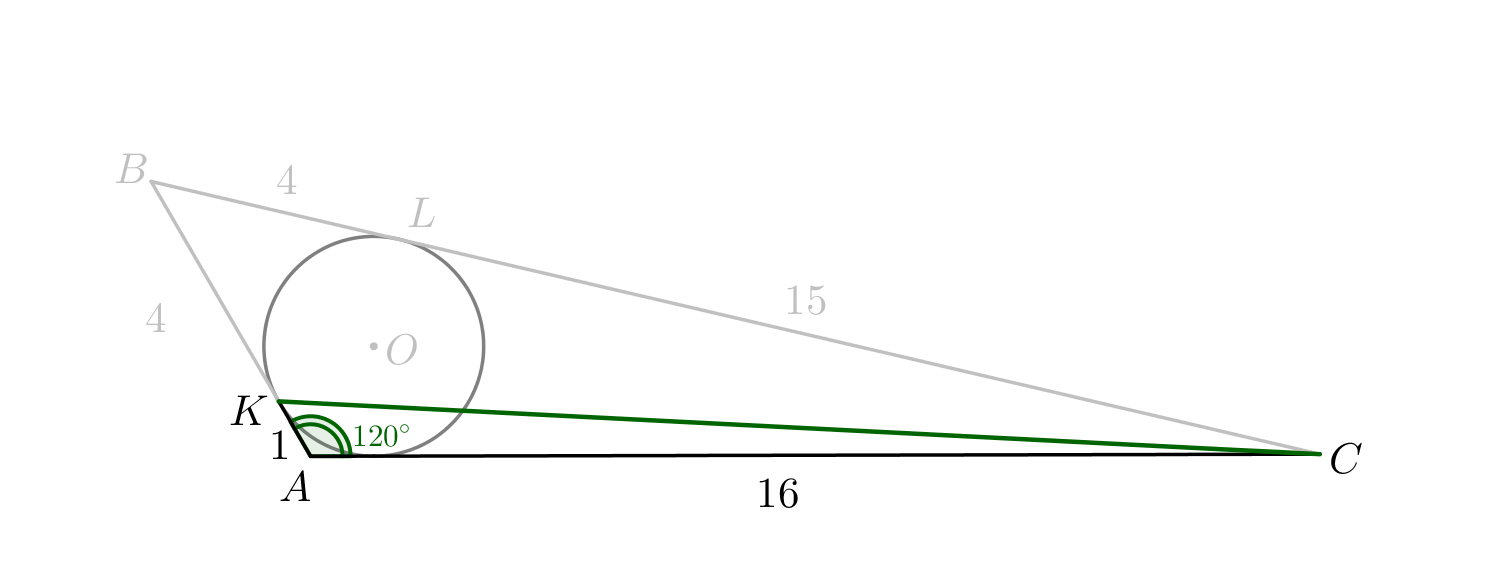
Запишем теорему косинусов для стороны \(\displaystyle CK{\small:}\)
\(\displaystyle CK^2=\left(1+15\right)^2+1^2-2\cdot\left(1+15\right)\cdot1\cdot\cos120^{\circ}\small.\)
Вычислим правую часть:
\(\displaystyle CK^2=16^2+1^2-2\cdot 16\cdot1\cdot\Big(-\frac{1}{2}\Big)\small,\)
\(\displaystyle CK^2=256+1+16\small,\)
\(\displaystyle CK^2=273\small,\)
\(\displaystyle CK=\sqrt{273}\small.\)
Ответ: \(\displaystyle CK=\sqrt{273}\small.\)