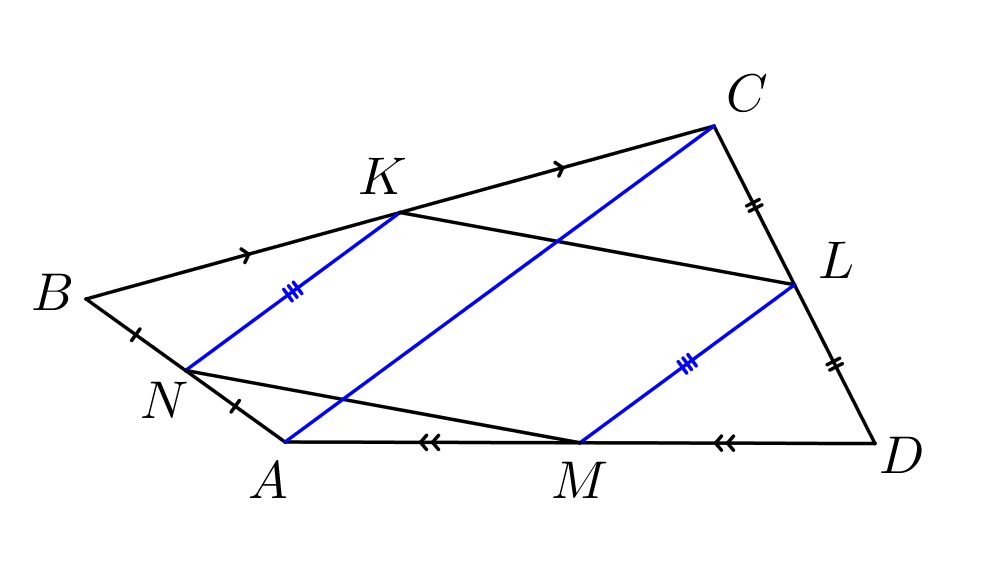
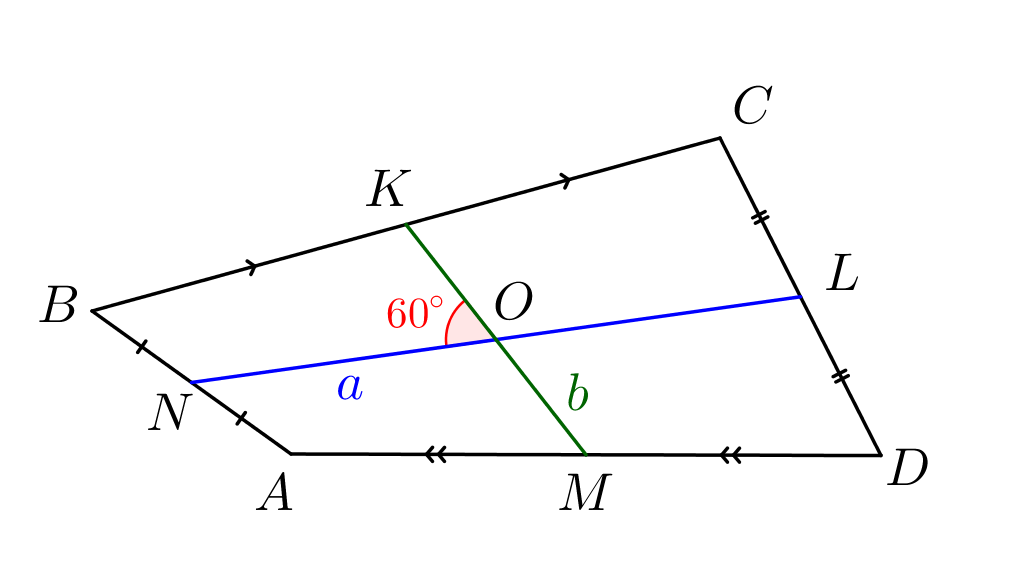
В выпуклом четырехугольнике отрезки, соединяющие середины противоположных сторон, равны \(\displaystyle a\) и \(\displaystyle b\) и пересекаются под углом \(\displaystyle 60^{\circ}\small.\) Найдите диагонали этого четырехугольника.
Проведем отрезки \(\displaystyle NK,\,ML\) и диагональ \(\displaystyle AC\small.\) Тогда \(\displaystyle NK\) – средняя линия треугольника \(\displaystyle ABC\) (\(\displaystyle AN=NB\) и \(\displaystyle CK=KB\)). Значит,
|
|
Аналогично, \(\displaystyle ML\) – средняя линия треугольника \(\displaystyle ACD\) (\(\displaystyle CL=LD\) и \(\displaystyle AM=MD\)). Значит,
|
Таким образом, получаем:
\(\displaystyle NK=ML=\frac{AC}{2}\) и \(\displaystyle NK||AC||ML\small.\)
Аналогично,
\(\displaystyle NM=KL=\frac{BD}{2}\) и \(\displaystyle NM||BD||KL\small.\)
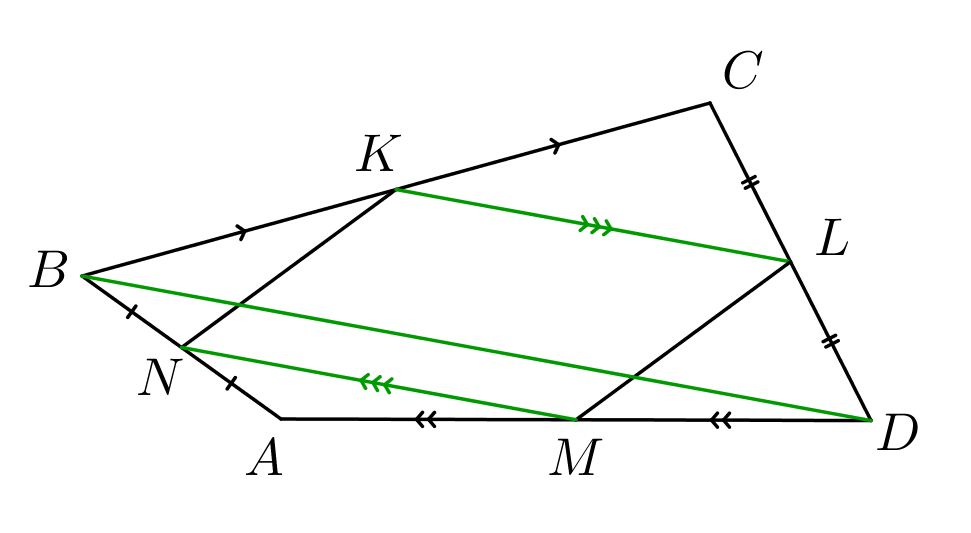
Значит, противоположные стороны четырехугольника \(\displaystyle KLMN\) равны и параллельны.
То есть \(\displaystyle KLMN\) – параллелограмм.
Также теперь, чтобы найти диагонали \(\displaystyle ABCD\small,\) достаточно найти стороны \(\displaystyle KLMN\small.\)
\(\displaystyle NK=\frac{\sqrt{a^2+b^2-ab}}{2}\) и \(\displaystyle NM=\frac{\sqrt{a^2+b^2+ab}}{2}\small.\)
В параллелограмме диагонали делятся точкой пересечения поплам: \(\displaystyle NO=LO=\frac{a}{2}\) и \(\displaystyle MO=KO=\frac{b}{2}\small.\) | 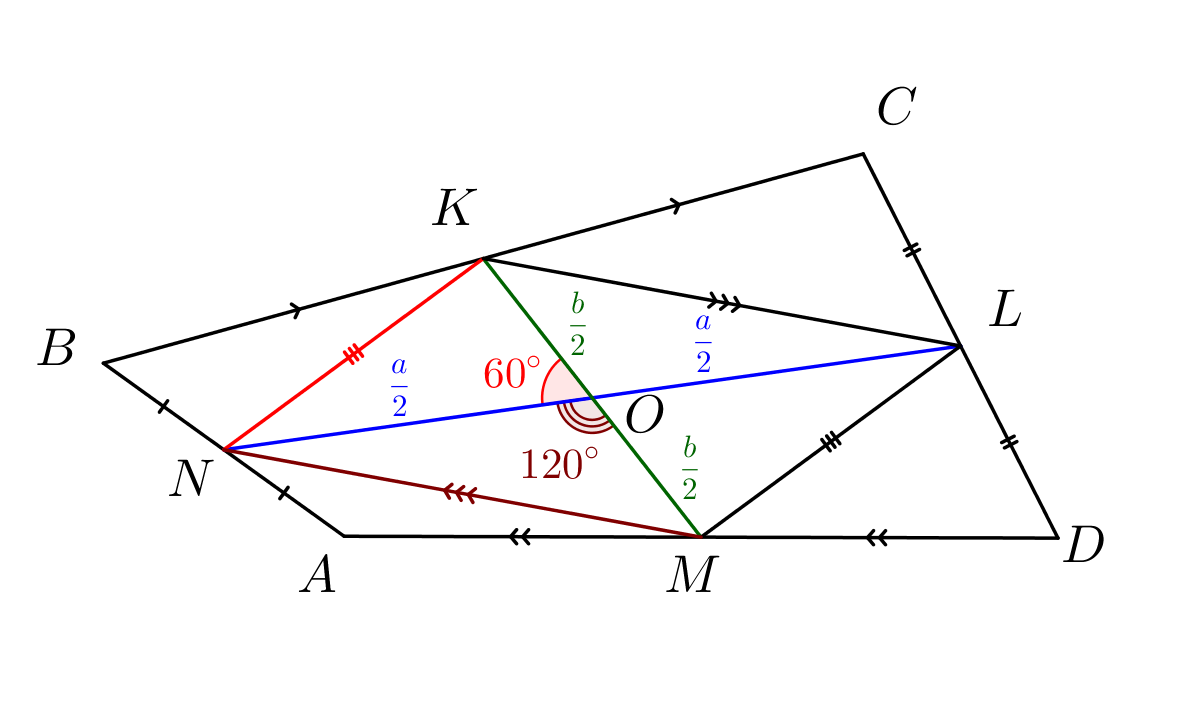 |
Тогда по теореме косинусов для треугольника \(\displaystyle NOK\small,\) получаем:
\(\displaystyle NK^2=\left(\frac{a}{2}\right)^2+\left(\frac{b}{2}\right)^2-2\cdot\frac{a}{2}\cdot \frac{b}{2}\cdot\cos60^{\circ}\small,\)
\(\displaystyle NK=\frac{\sqrt{a^2+b^2-ab}}{2}\small.\)
А по теореме косинусов для треугольника \(\displaystyle NOM\small,\) получаем:
\(\displaystyle NM^2=\left(\frac{a}{2}\right)^2+\left(\frac{b}{2}\right)^2-2\cdot\frac{a}{2}\cdot \frac{b}{2}\cdot\cos120^{\circ}\small,\)
\(\displaystyle NM=\frac{\sqrt{a^2+b^2+ab}}{2}\small.\)
Тогда
\(\displaystyle AC=2NK=\sqrt{a^2+b^2-ab}\) и \(\displaystyle BD=2NM=\sqrt{a^2+b^2+ab}\small.\)
Ответ: \(\displaystyle AC=\sqrt{a^2+b^2-ab}\) и \(\displaystyle BD=\sqrt{a^2+b^2+ab}\small.\)