На рисунке изображён равнобедренный треугольник \(\displaystyle ABC\) с отмеченными равными элементами.
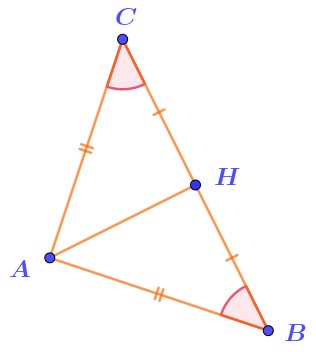
Какой отрезок называется основанием этого треугольника?
Основание треугольника \(\displaystyle ABC - \) отрезок
Равнобедренный треугольник
Треугольник называется равнобедренным, если две его стороны имеют равные длины.
Равные стороны называются боковыми сторонами, а третья сторона \(\displaystyle -\) основанием треугольника.
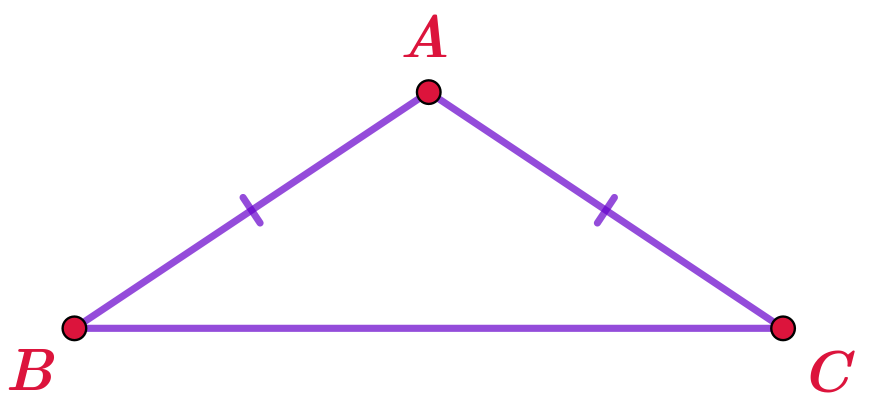
На рисунке изображен равнобедренный треугольник \(\displaystyle ABC\) с основанием \(\displaystyle BC{\small .}\)
В треугольнике \(\displaystyle ABC\)
\(\displaystyle AB{\small ,}\)\(\displaystyle BC\) и \(\displaystyle AC\,-\) стороны.
По условию,
\(\displaystyle AC=AB{\small .}\)
Значит, \(\displaystyle AB\) и \(\displaystyle AC\,-\) боковые стороны, а \(\displaystyle CB\,-\) основание треугольника \(\displaystyle ABC{\small .}\)
Ответ: \(\displaystyle BC{\small .}\)