На клетчатой бумаге отмечены несколько точек.
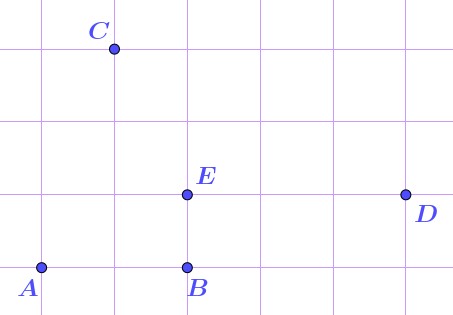
Какие треугольники из перечисленных являются равнобедренными?
Последовательно рассмотрим каждый треугольник.
| УТВЕРЖДЕНИЕ | ЧЕРТЁЖ | ВЫВОД |
| Треугольник \(\displaystyle ABC\,-\) равнобедренный | 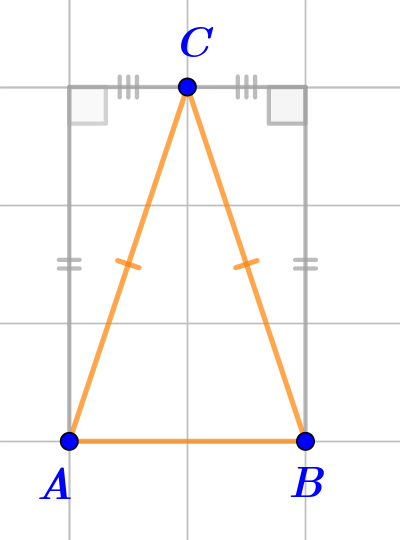 | ДА В треугольникe \(\displaystyle ABC\) боковые стороны \(\displaystyle AC\) и \(\displaystyle BC\) равны как стороны, противолежащие прямым углам в равных треугольниках. |
| Треугольник \(\displaystyle ABE\,-\) равнобедренный | 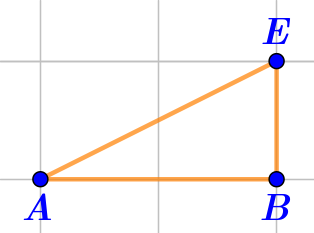 | НЕТ По рисунку видно, что в треугольнике \(\displaystyle ABE\) нет двух равных сторон. |
| Треугольник \(\displaystyle CBD\,-\) равнобедренный | 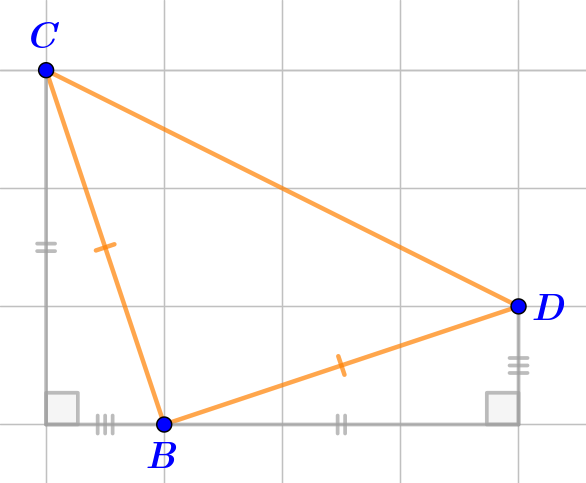 | ДА В треугольникe \(\displaystyle CBD\) боковые стороны \(\displaystyle BD\) и \(\displaystyle BC\) равны как стороны, противолежащие прямым углам в равных треугольниках. |
| Треугольник \(\displaystyle ACE\,-\) равнобедренный | 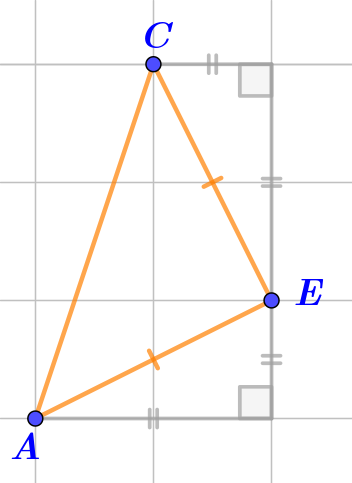 | ДА В треугольникe \(\displaystyle ACE\) боковые стороны \(\displaystyle AE\) и \(\displaystyle EC\) равны как стороны, противолежащие прямым углам в равных треугольниках. |
| Треугольник \(\displaystyle BDE\,-\) равнобедренный | 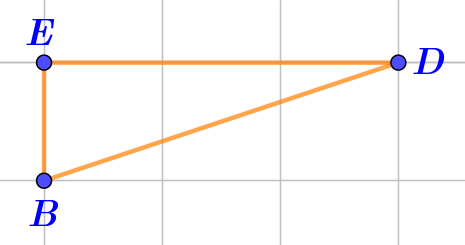 | НЕТ По рисунку видно, что в треугольнике \(\displaystyle BDE\) нет двух равных сторон. |
Ответ: \(\displaystyle {\bf\triangle}ABC{\small ,}\)\(\displaystyle {\bf\triangle}CBD{\small ,}\)\(\displaystyle {\bf\triangle}ACE{\small .}\)