На рисунке две точки принадлежат, а две не принадлежат проведённой прямой.

Заполните пропуски, указав верное взаимное расположение прямой \(\displaystyle k\) и точек \(\displaystyle M,\,Q,\,P,\,N{\small .}\)
| \(\displaystyle M\) \(\displaystyle k{\small ;}\) | \(\displaystyle N\) \(\displaystyle k{\small ;}\) | \(\displaystyle Q\) \(\displaystyle k{\small ;}\) | \(\displaystyle P\) \(\displaystyle k{\small .}\) |
При расстановке знаков руководствуемся правилом обозначения принадлежности.
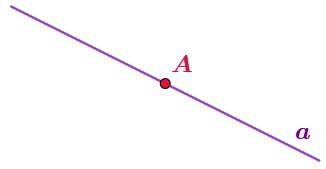
Запись \(\displaystyle A\in a\) означает, что точка \(\displaystyle A\) принадлежит прямой (или другой фигуре), обозначенной \(\displaystyle a{\small .}\)
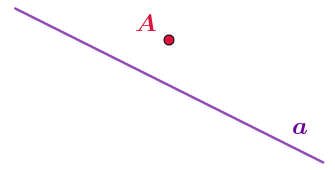
Запись \(\displaystyle A\notin a\) означает, что точка \(\displaystyle A\) не принадлежит прямой (или другой фигуре), обозначенной \(\displaystyle a{\small .}\)
Обращаем внимание на то, как направлен знак принадлежности.
Ответ: \(\displaystyle M\in k{\small ,\;\;\;} N\notin k{\small ,\;\;\;} Q\notin k{\small ,\;\;\;}P\in k{\small .}\)