Задание
На рисунке обозначены точка пересечения двух прямых, точка одной из прямых и ещё одна точка.
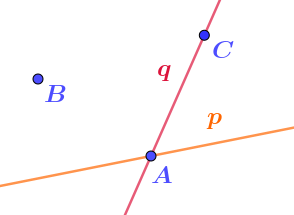
Укажите верное расположение точек \(\displaystyle A{\small ,\;}B\) и \(\displaystyle C\) по отношению к прямым \(\displaystyle p\) и \(\displaystyle q{\small .}\)
| \(\displaystyle A\) \(\displaystyle p{\small ;}\) | \(\displaystyle q\) \(\displaystyle C{\small ;}\) | \(\displaystyle B\) \(\displaystyle p{\small .}\) |
Решение
При расстановке знаков руководствуемся правилом обозначения принадлежности.
Сопоставим обозначенные на рисунке точки их описанию в условии.
- Точка пересечения двух прямых \(\displaystyle -\) точка \(\displaystyle A{\small .}\) Она принадлежит обеим прямым.
- Точка одной из прямых \(\displaystyle -\) точка \(\displaystyle C{\small .}\) Она, очевидно, не принадлежит прямой \(\displaystyle p{\small ,\;}\) а значит, принадлежит прямой \(\displaystyle q{\small .}\)
- Оставшаяся точка \(\displaystyle B\) явно не принадлежит каждой из двух прямых.
Последовательно выберем знаки в соответствии с установленными отношениями.
При выборе знака отношения следует внимательно следить за его направлением.
Ответ: \(\displaystyle A\in p{\small ,\;\;\;\;}q\ni C{\small ,\;\;\;\;}B\notin p{\small .}\)