Стороны треугольника равны \(\displaystyle 5,\,8\) и \(\displaystyle 9\small.\) Найдите радиус окружности, описанной около этого треугольника, если его площадь равна \(\displaystyle 6\sqrt{11}\small.\)
Воспользуемся формулой, связывающией длины сторон треугольника, его площадь и радиус описанной окружности.
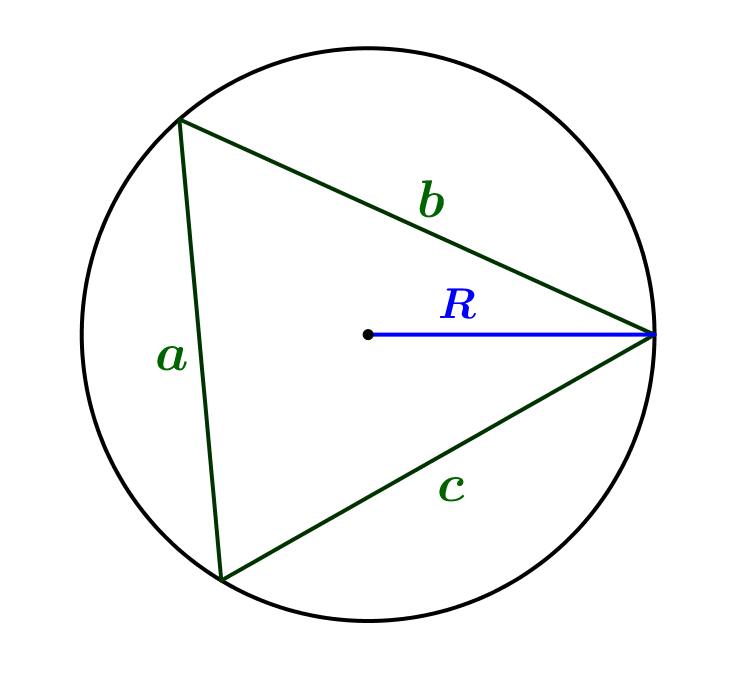
Если стороны треугольника \(\displaystyle a,\,b\) и \(\displaystyle c\small,\) а радиус описанной окружности \(\displaystyle R\small,\) то площадь треугольника:
\(\displaystyle S=\frac{abc}{4R}\small.\)
Подставляя данные из условия задачи, получаем:
\(\displaystyle 6\sqrt{11}=\frac{5\cdot8\cdot9}{4R}\small,\)
\(\displaystyle R=\frac{5\cdot8\cdot9}{4\cdot6\sqrt{11}}\small,\)
\(\displaystyle R=\frac{15}{\sqrt{11}}=\frac{15\sqrt{11}}{11}\small.\)
Ответ: \(\displaystyle R=\frac{15\sqrt{11}}{11}\small.\)