В окружность радиуса \(\displaystyle 14\) вписан четырехугольник \(\displaystyle ABCD\small.\) При этом \(\displaystyle AB=BC{ \small ,}\) \(\displaystyle \angle ADC=120^{\circ}\), и площадь треугольника \(\displaystyle BCD\) в два раза меньше площади треугольника \(\displaystyle ABD\small.\) Найдите все стороны четырехугольника \(\displaystyle ABCD\small.\)
Поскольку во вписанном четырехугольнике сумма противоположных углов равна \(\displaystyle 180^{\circ}\small,\) получаем: \(\displaystyle \angle ABC=180^{\circ}-\angle ADC=60^{\circ}\small.\)
Тогда все его стороны равны, и все углы равны \(\displaystyle 60^{\circ}\small.\)
\(\displaystyle \frac{AB}{\sin60^{\circ}}=2R,\) где \(\displaystyle R\) – радиус описанной окружности. Тогда \(\displaystyle AB=2R\sin60^{\circ}=14\sqrt{3}\small.\) То есть \(\displaystyle AB=BC=CA=14\sqrt{3}\small.\) | 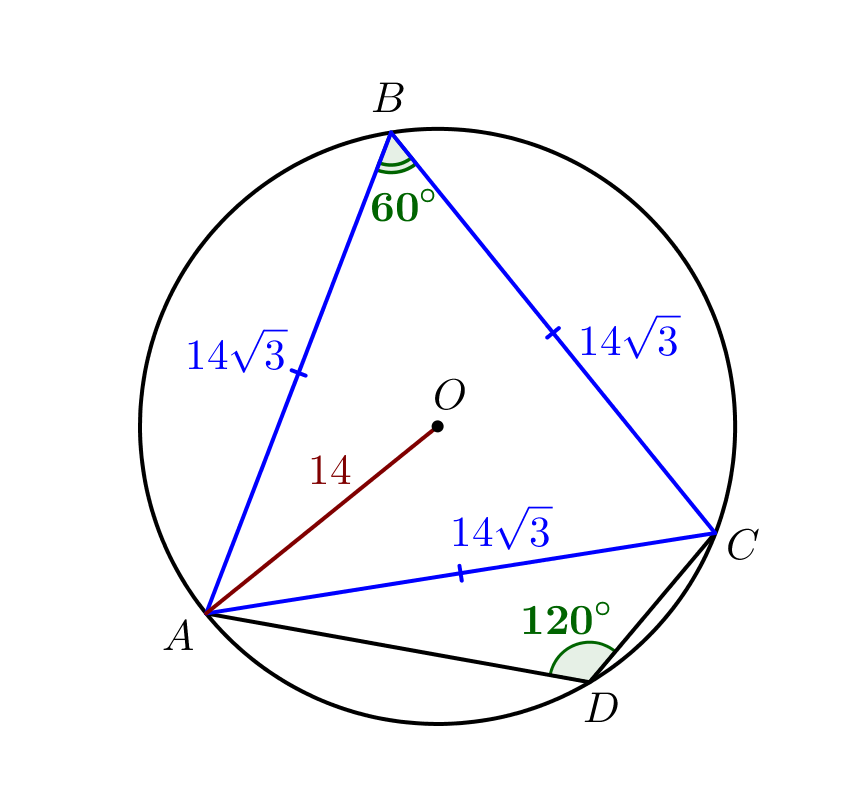 |
Остается найти две стороны четырехугольника.
Воспользуемся правилом вычисления площади:
\(\displaystyle S=\frac{abc}{4R}\small.\)
Тогда
\(\displaystyle S_{ABD}=\frac{AB\cdot BD\cdot AD}{4R}\) и \(\displaystyle S_{CBD}=\frac{CB\cdot BD\cdot CD}{4R}\small.\)
Поскольку площадь треугольника \(\displaystyle BCD\) в два раза меньше площади треугольника \(\displaystyle ABD\small,\) получаем:
\(\displaystyle \frac{AB\cdot BD\cdot AD}{4R}=2\cdot\frac{CB\cdot BD\cdot CD}{4R}\small.\)
Сокращаем равные множители и получаем:
\(\displaystyle AD=2CD\small.\)
Обозначим \(\displaystyle CD=x\) и запишем теорему косинусов для треугольника \(\displaystyle ACD{\small:}\) \(\displaystyle AC^2=AD^2+CD^2-2\cdot AD\cdot CD\cdot \cos120^{\circ}\small.\) Подставляя известные значения, получаем: \(\displaystyle \left(14\sqrt{3}\right)^2=(2x)^2+x^2-2x\cdot2x\cdot\left(-\frac{1}{2}\right)\small,\) \(\displaystyle 588=7x^2\small.\) Длина стороны неотрицательное число, поэтому: \(\displaystyle x=\sqrt{588:7}=2\sqrt{21}\small.\) | 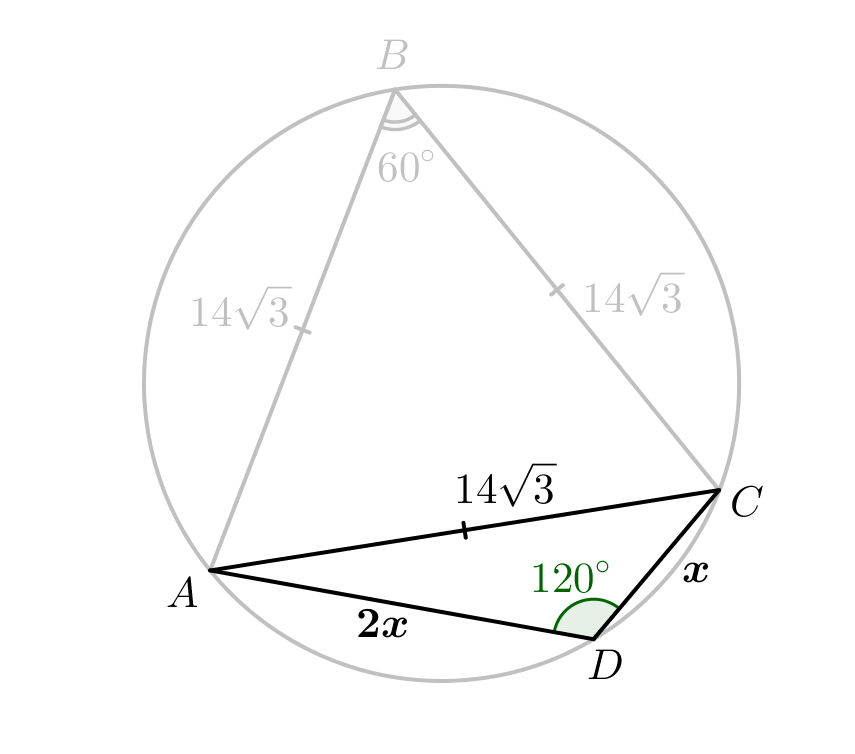 |
Таким образом, получаем стороны четырехугольника:
\(\displaystyle AB=BC=14\sqrt{3},\,AD=4\sqrt{21}\) и \(\displaystyle CD=2\sqrt{21}\small.\)
Ответ: \(\displaystyle AB=14\sqrt{3}\) и \(\displaystyle CD=2\sqrt{21}\small.\)