Периметр треугольника равен \(\displaystyle 47\,\footnotesize{см}\), а длины двух его сторон \(\displaystyle -\) \(\displaystyle 11\,\footnotesize{см}\) и \(\displaystyle 23\,\footnotesize{см}{\small .}\)
Выразите в сантиметрах длину третьей стороны треугольника.
\(\displaystyle {\footnotesize см}{\small.}\)
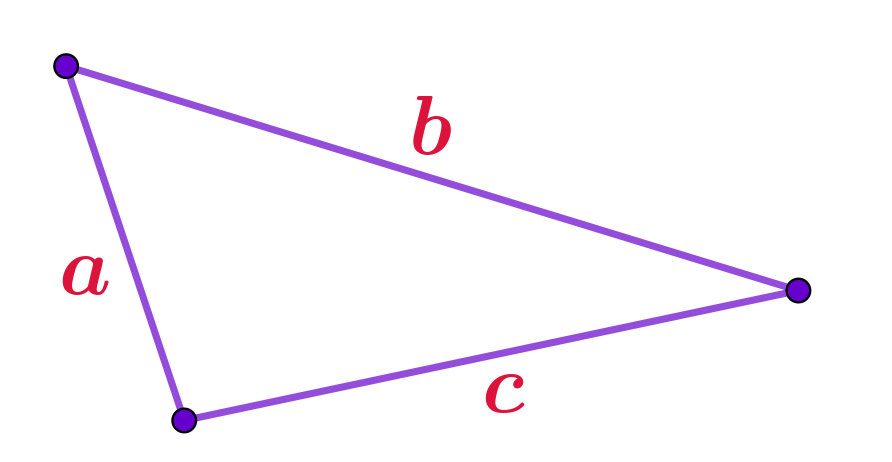
Периметр \(\displaystyle P\) треугольника равен сумме длин его сторон: \(\displaystyle P=\color{#DC143C}a+\color{#DC143C}b+\color{#DC143C}c{\small .}\) |
|
Чтобы найти неизвестную длину стороны треугольника, вычтем из периметра сумму длин остальных сторон:
\(\displaystyle c=P-(a+b)=47-(11+23)=\)\(\displaystyle 13\;({\footnotesize см})\)
Выполняя вычисления, важно помнить, что все линейные величины должны быть выражены в одинаковых единицах длины.
Например, в решённой задаче все вычисления производились в сантиметрах.
Ответ: \(\displaystyle 13\, {\footnotesize см}{\small.}\)