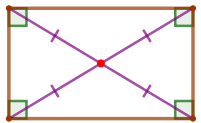
Диагонали \(\displaystyle AC\) и \(\displaystyle BD\) прямоугольника \(\displaystyle ABCD\) пересекаются в точке \(\displaystyle O{\small,}\) \(\displaystyle P_{\triangle OAB}=13\, {\footnotesize см}{\small,}\) \(\displaystyle P_{\triangle OAD}=14\, {\footnotesize см}{\small.}\) Найдите периметр данного прямоугольника, если длина диагонали \(\displaystyle AC\) равна \(\displaystyle 5\, {\footnotesize см}{\small.}\)
\(\displaystyle P_{ABCD}=\) \(\displaystyle {\footnotesize см}{\small.}\)
Требуется найти периметр данного прямоугольника. | 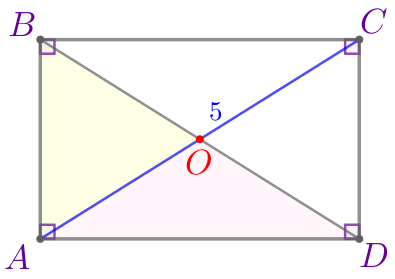 |
\(\displaystyle P_{ABCD}=2(AB+ AD){\small.}\)
Известны периметры треугольников \(\displaystyle AOB\) и \(\displaystyle AOD{\small:}\)
\(\displaystyle P_{\triangle OAB}=AB+OA+OB=13\, {\footnotesize см}{\small;}\)
\(\displaystyle P_{\triangle OAD}=AD+OA+OD=14\, {\footnotesize см}{\small.}\)
Выразим из этих равенств стороны \(\displaystyle AB\) и \(\displaystyle AD{\small:}\)
\(\displaystyle AB=13-(OA+OB){\small;}\)
\(\displaystyle AD=14-(OA+OD){\small.}\)
\(\displaystyle OA=OB=OC=OD=2{,}5\, \footnotesize см{\small.}\)
Тогда
\(\displaystyle AB=13-(2{,}5+2{,}5)=13-5=8\, \footnotesize см{\small;}\)
\(\displaystyle AD=14-(2{,}5+2{,}5)=14-5=9\, \footnotesize см{\small.}\)
Подставим в формулу периметра прямоугольника найденные длины сторон:
\(\displaystyle P_{ABCD}=2(AB+ AD){\small;}\)
\(\displaystyle P_{ABCD}=2 \cdot (8+ 9)=2 \cdot 17=34\, {\footnotesize см}{\small.}\)
Ответ: \(\displaystyle P_{ABCD}=34\, {\footnotesize см}{\small.}\)