Длина стороны клетки равна \(\displaystyle 1\)см. Найдите длину хорды \(\displaystyle AB\small.\)
Отметим на окружности точки \(\displaystyle C\) и \(\displaystyle D\small.\) Точка \(\displaystyle M\) лежит на хорде \(\displaystyle CD\) и делит ее пополам. |
Теорема об отрезках пересекающихся хорд
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды:
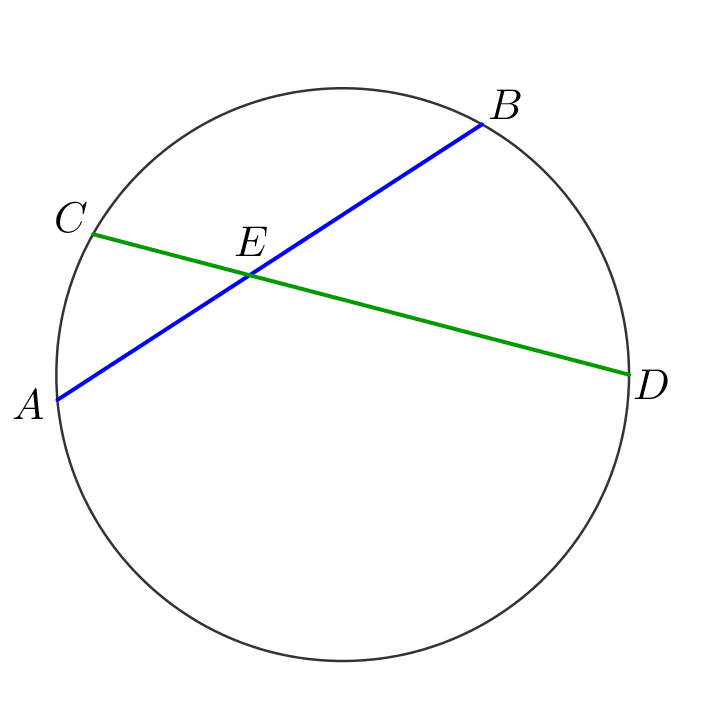
\(\displaystyle \color{blue}{AE}\cdot \color{blue}{BE}=\color{green}{CE}\cdot \color{green}{ DE}\)
Тогда, получаем:
\(\displaystyle AM\cdot BM=CM\cdot DM=CM^2\small.\)
Чтобы найти \(\displaystyle BM\small,\) найдем \(\displaystyle AM\) и \(\displaystyle CM\small.\)
Построим прямоугольный треугольник с гипотенузой \(\displaystyle AM\) и катетами, проходящими по линиям сетки. Катеты этого прямоугольного треугольника равны \(\displaystyle 1\)см и \(\displaystyle 3\)см. Тогда по теореме Пифагора: \(\displaystyle AM^2=1^2+3^2=10\small,\) \(\displaystyle AM=\sqrt{10}\)см. |
Подставим полученные значения:
\(\displaystyle \sqrt{10}\cdot BM=\left(\sqrt{5}\right)^2\small.\)
Находим \(\displaystyle BM{\small:}\)
\(\displaystyle BM=\frac{\left(\sqrt{5}\right)^2}{\sqrt{10}}=\frac{5}{\sqrt{10}}=\frac{\sqrt{10}}{2}\)см.
Тогда
\(\displaystyle AB=AM+BM=\sqrt{10}+\frac{\sqrt{10}}{2}=\frac{3\sqrt{10}}{2}\)см.
Ответ: \(\displaystyle AB=\frac{3\sqrt{10}}{2}\)см.