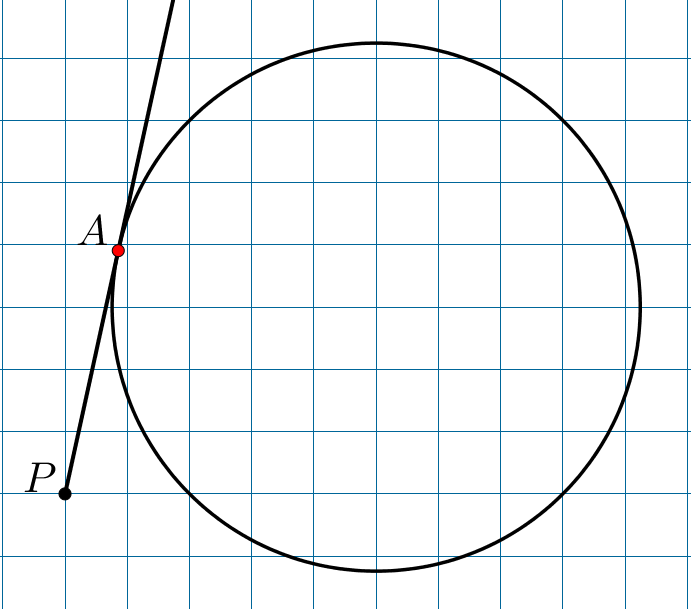
Длина стороны клетки равна \(\displaystyle 1\)см. Найдите длину отрезка \(\displaystyle AP\small.\)
Теорема об отрезках касательной и секущей
Если секущая и касательная проведены к окружности из одной точки, то квадрат расстояния до точки касания равен произведению отрезков секущей:
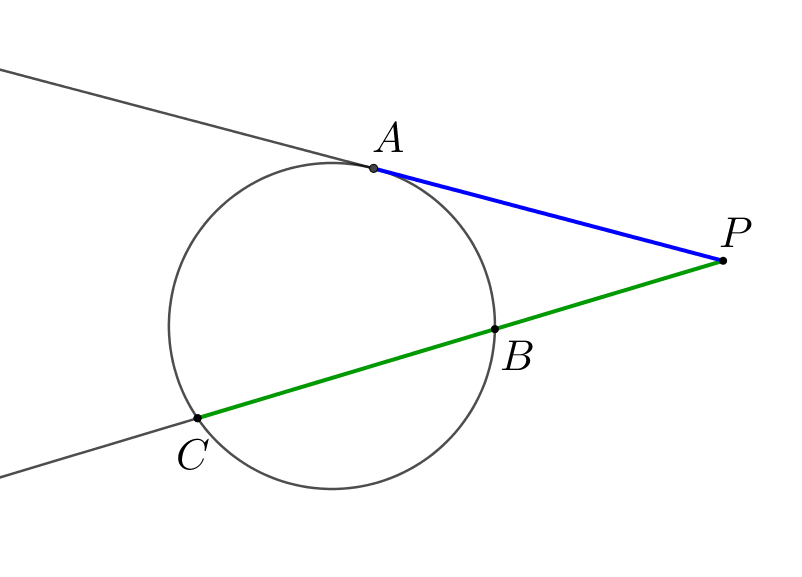
\(\displaystyle \color{blue}{AP^2}=\color{green}{BP}\cdot \color{green}{CP}\)
Проведем горизонтальную секущую к окружности через точку \(\displaystyle P\small.\) Точки пересечения этой секущей с окружностью обозначим за \(\displaystyle B\) и \(\displaystyle C\small,\) как показано на рисунке. Получаем: \(\displaystyle BP\cdot CP=AP^2\small.\) Длина стороны клетки равна \(\displaystyle 1\)см, тогда \(\displaystyle BP=2\)см и \(\displaystyle CP=8\)см. Подставляя, получаем: \(\displaystyle 2\cdot8=AP^2\small,\) \(\displaystyle AP=\sqrt{2\cdot8}=4\)см. | 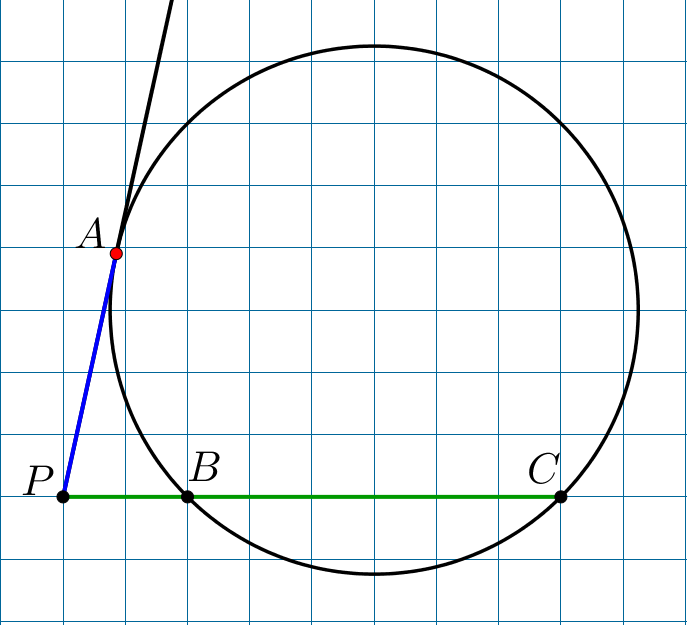 |
Ответ: \(\displaystyle AP=4\)см.