Про точки одной прямой известно следующее:
- точка \(\displaystyle E~-\) общая середина отрезков \(\displaystyle AC\) и \(\displaystyle BD{\normalsize ;}\)
- точка \(\displaystyle A~-\) середина отрезка \(\displaystyle DE{\small .}\)
Подпишите точки на рисунке в соответствии с этим описанием.
 | ||||
Точка \(\displaystyle E\) – общая середина отрезков \(\displaystyle AC\) и \(\displaystyle BD{\small .}\)
Значит, на прямой по обе стороны этой точки должно быть не меньше двух точек.
Такая точка на рисунке единственная. Подпишем её.

Видим, что точка \(\displaystyle D\) должна быть крайней.
Иначе на отрезке \(\displaystyle DE\) не будет отмеченной точки, которую можно было бы подписать как \(\displaystyle A{\small .}\)
Отмечаем соответствующие точки.

Точка \(\displaystyle E\) должна быть серединой отрезка \(\displaystyle BD{\small .}\)
Значит, точка \(\displaystyle B~-\) крайняя точка.
Остаётся убедиться в том, что оставшуюся точку можно подписать \(\displaystyle C{\small .}\)
Действительно, как раз получается, что точка \(\displaystyle E~-\) середина отрезка \(\displaystyle AC{\small .}\)

Определив, что точка \(\displaystyle D\) является крайней из отмеченных точек, мы разместили её на левом краю рисунка.
Мы могли бы выбрать и правый край.
В этом случае получается другое решение, которое также удовлетворяет условиям.

Ответ:
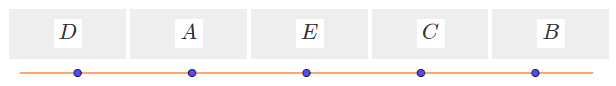
или